题目内容
【题目】如图所示,面![]() ,点A在直线
,点A在直线![]() 上的射影为
上的射影为![]() ,点B在直线
,点B在直线![]() 上的射影为
上的射影为![]() ,连接
,连接![]() ,已知
,已知![]() ,
,
(Ⅰ)求四面体![]() 的体积
的体积
(Ⅱ)求二面角![]() 的余弦.
的余弦.
![]()
【答案】(1)体积V=![]() (2)余弦值为
(2)余弦值为![]()
【解析】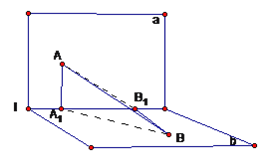
【试题分析】(1)先依据题设条件推证并确定四面体的底面与高,再求底面面积与高的值,运用三棱锥的体积公式进行求解;(2)建立空间直角坐标系,先求两个平面的法向量,运用向量的数量积公式求出两法向量的夹角的余弦,然后借助二面角的平面角与两法向量的夹角之间的关系求解:
解:(1)如图,因![]() ,又
,又![]() ,则
,则![]() ,又
,又![]() ,故
,故![]() ;同理可知:
;同理可知: ![]() ,所以
,所以![]() ,
, ![]() ,故四面体
,故四面体![]() 的体积
的体积![]() ;
;
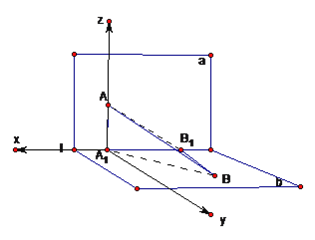
(2)建立如图所示的空间直角坐标系,则![]() ,所以
,所以![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则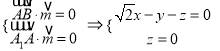 ,令
,令![]() ,故
,故![]() ;设平面
;设平面![]() 的法向量为
的法向量为![]() ,则
,则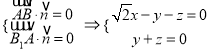 ,令
,令![]() ,故
,故![]() ,故由向量的数量积公式可得
,故由向量的数量积公式可得![]() ,而
,而![]() ,所以
,所以![]() ,由于两法向量所成的角与二面角的平面角互补,所以二面角
,由于两法向量所成的角与二面角的平面角互补,所以二面角![]() 的余弦值为
的余弦值为![]() 。
。

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目