Question

过曲线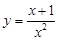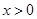（）上横坐标为1的点的切线方程为（   ）

A．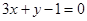

B．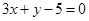

C．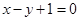

D．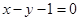

Answer 1

B

解析考点：利用导数研究曲线上某点切线方程．
分析：先求出切线的斜率，以及切点的坐标，点斜式写出切线方程，并化为一般式．
解：∵y′==，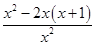
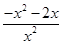∴该切线的斜率k=y’|_x="1" =-3，
曲线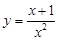（x＞0）上横坐标为1的点（1，2），
故所求的切线方程为y-2=-3（x-1），即 3x+y-5=0，
故答案为：B．
点评：本题考查求函数在某点的切线方程的求法，先求出切线的斜率及且点的坐标，从而得到切线方程．