题目内容
【题目】已知函数![]() 在
在![]() 处取得极值
处取得极值![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,若对任意的
,若对任意的![]() ,总存在唯一的
,总存在唯一的![]() (
(![]() 为自然对数的底数)使得
为自然对数的底数)使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】解: (1)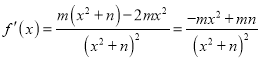 …………………………2分
…………………………2分
由![]() 在
在![]() 处取到极值2,故
处取到极值2,故![]() ,
,![]() 即
即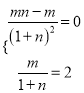 ,
,![]()
解得![]() ,经检验,此时
,经检验,此时![]() 在
在![]() 处取得极值.故
处取得极值.故![]() ……5分
……5分
(2)由(1)知 ,故
,故![]() 在
在![]() 上单调递增,在
上单调递增,在![]()
![]() 上单调递减,由
上单调递减,由![]() ,故
,故![]() 的值域为
的值域为![]() …………………………7分
…………………………7分
依题意![]() ,记
,记![]()
![]()
![]()
![]()
(ⅰ)当![]() 时,
时,![]()
![]()
![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
依题意由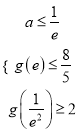 ,得
,得![]() ,……………………………………………………8分
,……………………………………………………8分
(ⅱ)当![]() 时,
时, ![]()
![]() 当
当![]() 时,
时, ![]()
![]() ,当
,当![]() 时,
时, ![]()
![]()
依题意得: 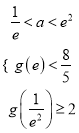 或
或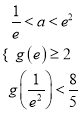 ,解得
,解得![]() ,…………………………10分
,…………………………10分
(ⅲ)当![]()
![]() 时,
时, ![]()
![]() ,此时
,此时![]()
![]() ,
,![]() 在
在![]() 上单调递增依题意得
上单调递增依题意得
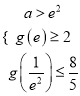 即
即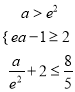 此不等式组无解 ……………………………………11分.
此不等式组无解 ……………………………………11分.
综上,所求![]() 取值范围为
取值范围为![]() ………………………………………………14分
………………………………………………14分
【解析】略

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 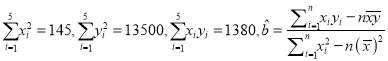 .
.
【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
销售天数(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).
