题目内容
若θ是三角形的一个内角,且函数y=cosθ•x2-4sinθ•x+6对于任意实数x均取正值,那么cosθ所在区间是( )
A、(
| ||
B、(0,
| ||
C、(-2,
| ||
D、(-1,
|
分析:根据题意可知需函数的图象开口向上需cosθ>0,同时判别式小于0,综合求得cosθ的范围.
解答:解:根据题意可知y=cosθ•x2-4sinθ•x+6>0恒成立,
∴要求
求得
<cosθ<1
故选A
∴要求
|
| 1 |
| 2 |
故选A
点评:本题主要考查了同角三角函数的基本关系的应用,函数恒成立问题,二次函数性质等.考查了学生对函数思想的运用,三角函数基础知识的运用.

练习册系列答案
相关题目
 =2”.若把该结论推广到正四面体(所有棱长均相等的三棱锥),则有结论:“在正四面体ABCD中,若M是正三角形BCD的中心,O是在正四面体ABCD内切球的球心,则
=2”.若把该结论推广到正四面体(所有棱长均相等的三棱锥),则有结论:“在正四面体ABCD中,若M是正三角形BCD的中心,O是在正四面体ABCD内切球的球心,则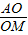 = ”.
= ”. ,那么这个球的表面积是 .
,那么这个球的表面积是 .