题目内容
函数 的图象大致为( )
的图象大致为( )
A
解析试题分析:函数的定义域为R。 为奇函数,排除C,D。
为奇函数,排除C,D。 ,所以当x较小时,函数为减函数,而后为增函数,故选A。
,所以当x较小时,函数为减函数,而后为增函数,故选A。
考点:本题主要考查函数的奇偶性,应用导数研究函数的单调性。
点评:简单题,利用导数研究函数的单调性,是导数的基本应用问题。导数非负,函数为增函数,导数非正,函数为减函数。

练习册系列答案
相关题目
已知 ,
,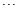
 则
则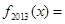 ( )
( )
A. | B.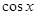 | C. | D.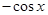 |
若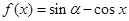 ,则
,则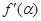 等于( )
等于( )
A.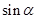 | B.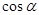 | C.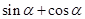 | D.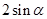 |
曲线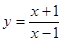 在点
在点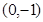 处的切线方程为( )
处的切线方程为( )
A.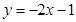 | B.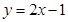 | C.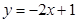 | D.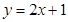 |
若曲线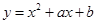 在点
在点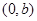 处的切线方程是
处的切线方程是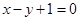 ,则( )
,则( )
A.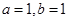 | B.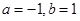 |
C.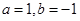 | D.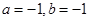 |
已知函数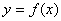 在
在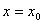 处可导,则
处可导,则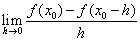 等于
等于
A.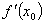 | B.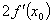 | C.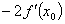 | D.0 |
由曲线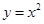 与
与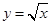 的边界所围成区域的面积为
的边界所围成区域的面积为
A.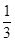 | B.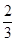 | C.1 | D.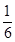 |
若函数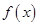 在R 上可导,且满足
在R 上可导,且满足 ,则( )
,则( )
A.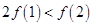 | B.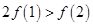 | C.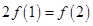 | D.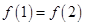 |
 为曲线
为曲线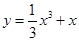 上的任意一点,在点
上的任意一点,在点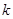 ,则
,则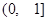 B
B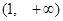 C.
C.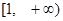 D.
D.