题目内容
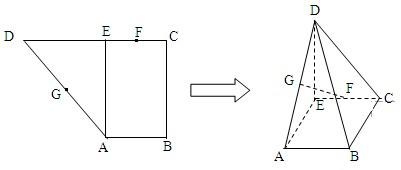
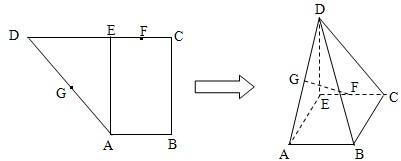
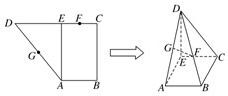
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+ ,过A作AE⊥CD.垂足为E,G,F分别为AD,CE的中点,现将△ADE沿AE折叠,使得DE⊥EC,
,过A作AE⊥CD.垂足为E,G,F分别为AD,CE的中点,现将△ADE沿AE折叠,使得DE⊥EC,
(Ⅰ)求证:FG∥面BCD;
(Ⅱ)设四棱锥D-ABCE的体积为V,其外接球体积为V′,求V:V′的值。
 ,过A作AE⊥CD.垂足为E,G,F分别为AD,CE的中点,现将△ADE沿AE折叠,使得DE⊥EC,
,过A作AE⊥CD.垂足为E,G,F分别为AD,CE的中点,现将△ADE沿AE折叠,使得DE⊥EC, (Ⅰ)求证:FG∥面BCD;
(Ⅱ)设四棱锥D-ABCE的体积为V,其外接球体积为V′,求V:V′的值。

(Ⅰ)证明:取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD,
∴面FHG∥面BCD,
∴GF∥面BCD。
(Ⅱ)解:V= ,
,
又外接球半径 ,
,
∴ ,
,
∴ 。
。
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD,
∴面FHG∥面BCD,
∴GF∥面BCD。
(Ⅱ)解:V=
 ,
,又外接球半径
 ,
,∴
 ,
, ∴
 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+ 已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足
已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=