题目内容
已知椭圆
+y2=1上一点M到点（1，0）的距离是
，则点M到直线x=-2的距离是（ ）A．
B．2
C．3
D．5
【答案】分析：由题意可知a=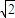
，b=c=1，（1，0）为椭圆的右焦点，x=-2问为椭圆的左准线，要求椭圆上的点M到左准线x=-2的距离，可先求其到右准线的距离，已知道点M到右焦点的距离，可利用第二定义即可
解答：解：由题意可得，椭圆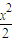
+y2=1中，a=
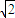，b=c=1
∴F（1，0）为椭圆的右焦点，离心率e=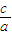
=
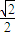，准线x=
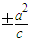=±2
∵M到右焦点（1，0）的距离是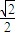
，由椭圆的第二定义可得，
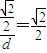（d为M到右准线的距离）
∴d=1
∵两准线间的距离为4
∴点M到直线x=-2即椭圆的左准线的距离为4-1=3
故选C
点评：本题主要考察了由椭圆方程求解椭圆的性质，解题主要是把所求的距离转化为求椭圆上一点到右准线的距离，第二定义的应用是解答本题的关键
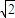，b=c=1，（1，0）为椭圆的右焦点，x=-2问为椭圆的左准线，要求椭圆上的点M到左准线x=-2的距离，可先求其到右准线的距离，已知道点M到右焦点的距离，可利用第二定义即可解答：解：由题意可得，椭圆
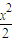+y2=1中，a=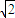，b=c=1∴F（1，0）为椭圆的右焦点，离心率e=
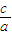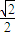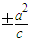=，准线x==±2∵M到右焦点（1，0）的距离是
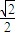，由椭圆的第二定义可得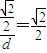，（d为M到右准线的距离）∴d=1
∵两准线间的距离为4
∴点M到直线x=-2即椭圆的左准线的距离为4-1=3
故选C
点评：本题主要考察了由椭圆方程求解椭圆的性质，解题主要是把所求的距离转化为求椭圆上一点到右准线的距离，第二定义的应用是解答本题的关键
练习册系列答案
高中必刷题系列答案
相关题目
+y2=1的左、右焦点为F1、F2，上顶点为A，直线AF1交椭圆于B．如图所示沿x轴折起，使得平面AF1F2⊥平面BF1F2．点O为坐标原点．
+y2=1（a＞1）的两个焦点为F1、F2，P为椭圆上一点，且∠F1PF2=60°，则|PF1|•|PF2|的值为（ ）
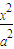+y2=1（a＞1）的两个焦点为F1、F2，P为椭圆上一点，且∠F1PF2=60°，则|PF1|•|PF2|的值为（ ）
