题目内容
已知函数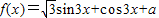 过点
过点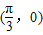 .
.(1)求a的值及函数y=f(x)的最小正周期;
(2)若
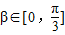 且
且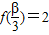 ,求
,求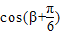 的值.
的值.
【答案】分析:(1)由函数图象过(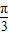 ,0),将此点坐标代入函数解析式,利用特殊角的三角函数值化简,求出a的值确定出f(x)解析式,找出ω的值,代入周期公式即可求出函数的最小正周期;
,0),将此点坐标代入函数解析式,利用特殊角的三角函数值化简,求出a的值确定出f(x)解析式,找出ω的值,代入周期公式即可求出函数的最小正周期;
(2)由f(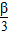 )=2及函数解析式,得到sin(β+
)=2及函数解析式,得到sin(β+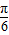 )的值,由β的范围求出β+
)的值,由β的范围求出β+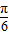 的范围,利用同角三角函数间的基本关系即可求出cos(β+
的范围,利用同角三角函数间的基本关系即可求出cos(β+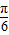 )的值.
)的值.
解答:解:(1)依题意将(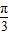 ,0)代入函数解析式得:
,0)代入函数解析式得:
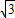 sin(3×
sin(3×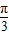 )+cos(3×
)+cos(3×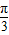 )+a=0,
)+a=0,
解得:a=1,
∴f(x)=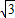 sin3x+cos3x+1=2sin(3x+
sin3x+cos3x+1=2sin(3x+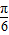 )+1,
)+1,
∵ω=3,
∴T=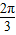 ;
;
(2)∵f(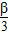 )=2sin(3×
)=2sin(3×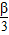 +
+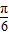 )+1=2,
)+1=2,
∴sin(β+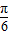 )=
)= ,
,
∵β∈[0,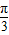 ],∴β+
],∴β+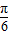 ∈[
∈[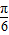 ,
,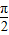 ],
],
∴cos(β+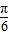 )=
)=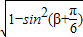 =
=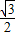 .
.
点评:此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,三角函数的周期性及其求法,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.
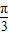 ,0),将此点坐标代入函数解析式,利用特殊角的三角函数值化简,求出a的值确定出f(x)解析式,找出ω的值,代入周期公式即可求出函数的最小正周期;
,0),将此点坐标代入函数解析式,利用特殊角的三角函数值化简,求出a的值确定出f(x)解析式,找出ω的值,代入周期公式即可求出函数的最小正周期;(2)由f(
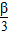 )=2及函数解析式,得到sin(β+
)=2及函数解析式,得到sin(β+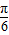 )的值,由β的范围求出β+
)的值,由β的范围求出β+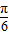 的范围,利用同角三角函数间的基本关系即可求出cos(β+
的范围,利用同角三角函数间的基本关系即可求出cos(β+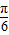 )的值.
)的值.解答:解:(1)依题意将(
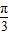 ,0)代入函数解析式得:
,0)代入函数解析式得: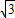 sin(3×
sin(3×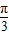 )+cos(3×
)+cos(3×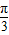 )+a=0,
)+a=0,解得:a=1,
∴f(x)=
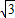 sin3x+cos3x+1=2sin(3x+
sin3x+cos3x+1=2sin(3x+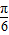 )+1,
)+1,∵ω=3,
∴T=
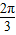 ;
;(2)∵f(
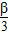 )=2sin(3×
)=2sin(3×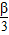 +
+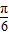 )+1=2,
)+1=2,∴sin(β+
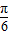 )=
)= ,
,∵β∈[0,
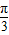 ],∴β+
],∴β+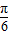 ∈[
∈[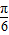 ,
,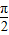 ],
],∴cos(β+
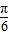 )=
)=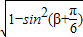 =
=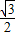 .
.点评:此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,三角函数的周期性及其求法,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
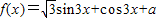 过点
过点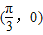 .
.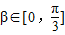 且
且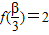 ,求
,求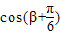 的值.
的值. 过点P(1,5),
过点P(1,5),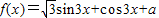 过点
过点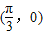 .
.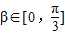 且
且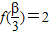 ,求
,求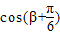 的值.
的值. 过点
过点 .
. 且
且 ,求
,求 的值.
的值.