Question

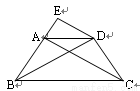
如图，等腰梯形ABCD的三边AB，BC，CD分别与函数y=-

1

2

x2+2，x∈[-2，2]的图象切于点P，Q，R．求梯形ABCD面积的最小值．

Answer 1

分析：设梯形ABCD的面积为s，点P的坐标为(t，-

1

2

t2+2)(0＜t≤2)，我们易求出直线AB的方程，进而求出A，B的坐标，进而得到梯形的上底、下底及高，代入梯形面积公式，利用基本不等式求出最值即可得到答案．

解答：解：设梯形ABCD的面积为s，点P的坐标为(t，-

1

2

t2+2)(0＜t≤2)．
由题意得，点Q的坐标为（0，2），直线BC的方程为y=2．
∵y=-

1

2

x2+2，∴y'=-x∴y'|_x=t=-t…（3分）
∴直线AB的方程为y-(-

1

2

t2+2)=-t(x-t)，
即：y=-tx+

1

2

t2+2…（5分）
令y=0得，x=

t2+4

2t

，∴A(

t2+4

2t

，0)．
令y=2得，x=

1

2

t∴B(

1

2

t，2)∴S=

1

2

×(

1

2

t+

t2+4

2t

)×2×2=2(t+

2

t

)≥4

2

…（8分）
当且仅当t=

2

t

，即t=

2

时，取“=”且

2

∈(0，2]，∴t=

2

时，S有最小值为4

2

．∴梯形ABCD的面积的最小值为4

2

…（12分）

点评：本题考查的知识点是导数与直线的斜率，二次函数的图象与性质，其中根据函数的解析式，求出导函数，进而求出过切点P的切线方程，是解答本题关键．