题目内容
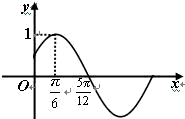 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若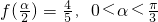 ,求cosα的值.
,求cosα的值.
 解:(Ⅰ)由图象知A=1
解:(Ⅰ)由图象知A=1f(x)的最小正周期T=4×(
 -
- )=π,故ω=
)=π,故ω= =2
=2将点(
 ,1)代入f(x)的解析式得sin(
,1)代入f(x)的解析式得sin( +φ)=1,
+φ)=1,又|φ|<
 ,∴φ=
,∴φ=
故函数f(x)的解析式为f(x)=sin(2x+
 )
)(Ⅱ)f(
 )=
)= ,即sin(
,即sin(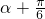 )=
)= ,注意到0<a<
,注意到0<a< ,则
,则 <
<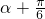 <
< ,
,所以cos(α+
 )=
)= .
.又cosα=[(α+
 )-
)- ]=cos(α+
]=cos(α+ )cos
)cos +sin(α+
+sin(α+ )sin
)sin =
=
分析:(I)观察图象可得函数的最值为1,且函数先出现最大值可得A=1;函数的周期T=π,结合周期公式T=
 可求ω;由函数的图象过(
可求ω;由函数的图象过( )代入可得φ
)代入可得φ(II)由(I)可得f(x)=sin(2x+
 ),从而由f(
),从而由f( )=
)= ,代入整理可得sin(
,代入整理可得sin(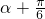 )=
)= ,结合已知0<a<
,结合已知0<a< ,可得cos(α+
,可得cos(α+ )=
)= .,利用
.,利用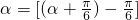 ,代入两角差的余弦公式可求
,代入两角差的余弦公式可求点评:本题主要考查了(i)由三角函数的图象求解函数的解析式,其步骤一般是:由函数的最值求解A,(但要判断是先出现最大值或是最小值,从而判断A的正负号)由周期求解ω=
 ,由函数图象上的点(一般用最值点)代入求解φ;
,由函数图象上的点(一般用最值点)代入求解φ;(ii)三角函数的同角平方关系,两角差的余弦公式,及求值中的拆角的技巧,要掌握常见的拆角技巧:①2α=(α+β)+(α-β)②2β=(α+β)-(α-β)③α=(α+β)-β④β=(α+β)-α

练习册系列答案
相关题目