Question

渔船甲在海中某岛南偏西50°方向,与岛相距12海里,看到渔船乙刚从岛向北偏西10°的方向航行,测得其速度为10海里/小时,问渔船甲需用多大速度朝什么方向航行,才能经过2小时追及渔船乙?

Answer 1

解:如右图,设A为岛的位置,B为渔船甲的位置,C为渔船甲追及渔船乙的位置.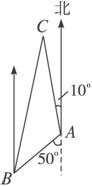

又设渔船甲追及渔船乙的速度为x海里/小时.

则BC=2x海里,AC=20海里.

在△ABC中，AB=12,∠CAB=180°-(50°+10°)=120°.

由余弦定理得BC²=AB²+AC²-2AB·AC·cos120°,即4x²=12²+20²+2×12×20×.

解之得x=14海里/小时.

由正弦定理得

sinB=≈0.619.

查表得∠B=38°13′,所求的方向为50°-38°13′=11°47′.

故渔船甲需用14海里/小时的速度朝北偏东11°47′航行2小时才能追及渔船乙.