题目内容
集合A是由具备下列性质的函数f (x)组成的:①函数f (x)的定义域是[0,+∞);②函数f(x)的值域是[-2,4);③函数f(x)在[0,+∞)上是增函数.试分别探究下列两小题:
(1)判断函数 ,及
,及 是否属于集合A,并简要说明理由;
是否属于集合A,并简要说明理由;
(2)对于(1)中你认为属于集合A的函数f(x),不等式f(x)+f(x+2)<2f(x+1)是否对于任意的x≥0总成立?若不成立,说明理由?若成立,请证明你的结论.
解:(1)∵函数 的值域[-2,+∞)
的值域[-2,+∞)
∴f1(x)∉A
对于f2(x),定义域为[0,+∞),满足条件①.而由x≥0知 ,
,
∴ ,满足条件②
,满足条件②
又∵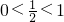 ,
,
∴ 在[0,+∞)上是减函数.
在[0,+∞)上是减函数.
∴f2(x)在[0,+∞)上是增函数,满足条件③
∴f2(x)属于集合A.
(2)由(1)知,f2(x)属于集合A.
∴原不等式为
整理为: .
.
∵对任意 ,
,
∴原不等式对任意x≥0总成立
分析:(1)由已知可得函数 的值域[-2,+∞),从而可得f1(x)∉A,对于f2(x),只要分别判断函数定义域是否满足条件①.值域是否满足条件②,单调性是否满足条件③,即可得答案;
的值域[-2,+∞),从而可得f1(x)∉A,对于f2(x),只要分别判断函数定义域是否满足条件①.值域是否满足条件②,单调性是否满足条件③,即可得答案;
(2)由(1)知,f2(x)属于集合A.原不等式为 ,通过整理不等式可判断.
,通过整理不等式可判断.
点评:本题目以新定义为载体主要综合考查了函数的定义域、值域、复合函数的单调性的求解及判断,属于函数知识的综合应用.
 的值域[-2,+∞)
的值域[-2,+∞)∴f1(x)∉A
对于f2(x),定义域为[0,+∞),满足条件①.而由x≥0知
 ,
,∴
 ,满足条件②
,满足条件②又∵
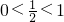 ,
,∴
 在[0,+∞)上是减函数.
在[0,+∞)上是减函数.∴f2(x)在[0,+∞)上是增函数,满足条件③
∴f2(x)属于集合A.
(2)由(1)知,f2(x)属于集合A.
∴原不等式为

整理为:
 .
.∵对任意
 ,
,∴原不等式对任意x≥0总成立
分析:(1)由已知可得函数
 的值域[-2,+∞),从而可得f1(x)∉A,对于f2(x),只要分别判断函数定义域是否满足条件①.值域是否满足条件②,单调性是否满足条件③,即可得答案;
的值域[-2,+∞),从而可得f1(x)∉A,对于f2(x),只要分别判断函数定义域是否满足条件①.值域是否满足条件②,单调性是否满足条件③,即可得答案;(2)由(1)知,f2(x)属于集合A.原不等式为
 ,通过整理不等式可判断.
,通过整理不等式可判断.点评:本题目以新定义为载体主要综合考查了函数的定义域、值域、复合函数的单调性的求解及判断,属于函数知识的综合应用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 -2(x≥0)及f2(x)=4-6·
-2(x≥0)及f2(x)=4-6· x(x≥0)是否属于集合A?并简要说明理由;
x(x≥0)是否属于集合A?并简要说明理由;