题目内容
已知x= 是
是 的一个极值点
的一个极值点
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调增区间;
的单调增区间;
(Ⅲ)设 ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
 是
是 的一个极值点
的一个极值点(Ⅰ)求
 的值;
的值;(Ⅱ)求函数
 的单调增区间;
的单调增区间;(Ⅲ)设
 ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?(1) b=" -1" (2)  (3) 过点(2,5)可作2条曲线y=g(x)的切线
(3) 过点(2,5)可作2条曲线y=g(x)的切线
 (3) 过点(2,5)可作2条曲线y=g(x)的切线
(3) 过点(2,5)可作2条曲线y=g(x)的切线试题分析:解:(1) 因x=-1是
 的一个极值点
的一个极值点∴
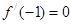
即 2+b-1=0
∴b= -1经检验,适合题意,所以b= -1. (7分)
(2)

∴
 >0
>0∴
 >0
>0∴x>
 ∴函数的单调增区间为
∴函数的单调增区间为 (14分)
(14分)(3)
 =2x+lnx
=2x+lnx设过点(2,5)与曲线g (x)的切线的切点坐标为

∴

即
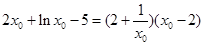 ∴
∴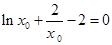
令h(x)=
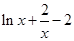
∴
 =
= =0
=0∴

∴h(x)在(0,2)上单调递减,在(2,
 )上单调递增
)上单调递增 又
又 ,h(2)=ln2-1<0,
,h(2)=ln2-1<0,
∴h(x)与x轴有两个交点
∴过点(2,5)可作2条曲线y=g(x)的切线. ……(16分)
点评:本试题主要是考查了导数的几何意义,以及函数极值和最值的运用,属于基础题。

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
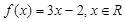 规定:给出一个实数
规定:给出一个实数 ,赋值
,赋值 ,若
,若 ,则继续赋值
,则继续赋值 , ,
, , 以此类推,若
以此类推,若 ,则
,则 ,否则停止赋值,如果得到
,否则停止赋值,如果得到 称为赋值了
称为赋值了 次
次 .已知赋值了
.已知赋值了 次后停止,则
次后停止,则


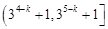
 ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线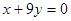 垂直。
垂直。 的值;
的值;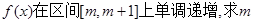 的取值范围。
的取值范围。 在
在 上两个零点,则
上两个零点,则 的取值范围为( )
的取值范围为( )



 中,若
中,若 ,则
,则 的值是
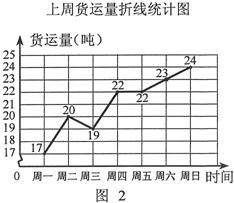
的值是  吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
 汽(元)和
汽(元)和 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份, )的函数解析式.
)的函数解析式. 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求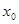 附近的左侧
附近的左侧 ,右侧
,右侧 ,那么
,那么 是极大值
是极大值