题目内容
下列命题中,真命题是( )A.?x∈R,使得sinx+cosx=1.5
B.
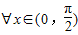 ,使得sinx>cos
,使得sinx>cosC.?x∈R,使得x2+x=-1
D.?x∈(0,+∞),使得ex>1+
【答案】分析:根据正弦型函数的值域,我们可以判定A的真假;根据正弦函数、余弦函数的图象与性质,我们可以判断B的真假;根据二次函数的性质,我们可以判断C的真假;根据导数工具,可以判断D的真假,进而得到答案.
解答:解:∵sinx+cosx=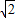 sin(x+
sin(x+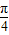 )∈[-
)∈[-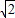 ,
,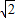 ],而1.5>
],而1.5>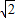 ,故A错误;
,故A错误;
当x∈(0,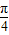 ]时,sinx≤cosx,故B错误;
]时,sinx≤cosx,故B错误;
当x2+x=-1时,x2+x+1=0,但其△=1-4=-3<0.故C不正确;
对于D:设f(x)=ex-x-1,则f′(x)=ex-1,
∴当x=0时,f′(x)=0,f(x)=0.
当x>0时,f′(x)>0,
∴f(x)在(0,+∞)上是增函数,
∴f(x)>f(0)=0.
∴对x∈(0,+∞),都有f(x)>0,
∴ex>x+1.故D正确;
故选D.
点评:本题考查的知识点是正弦型函数的值域,正弦型函数的单调性,不等式的性质,全称命题和特特命题,如何判断全(特)称命题的真假,是解答本题的关键.
解答:解:∵sinx+cosx=
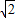 sin(x+
sin(x+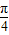 )∈[-
)∈[-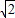 ,
,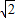 ],而1.5>
],而1.5>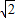 ,故A错误;
,故A错误;当x∈(0,
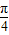 ]时,sinx≤cosx,故B错误;
]时,sinx≤cosx,故B错误;当x2+x=-1时,x2+x+1=0,但其△=1-4=-3<0.故C不正确;
对于D:设f(x)=ex-x-1,则f′(x)=ex-1,
∴当x=0时,f′(x)=0,f(x)=0.
当x>0时,f′(x)>0,
∴f(x)在(0,+∞)上是增函数,
∴f(x)>f(0)=0.
∴对x∈(0,+∞),都有f(x)>0,
∴ex>x+1.故D正确;
故选D.
点评:本题考查的知识点是正弦型函数的值域,正弦型函数的单调性,不等式的性质,全称命题和特特命题,如何判断全(特)称命题的真假,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
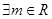 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1