题目内容
已知:函数f(x)=2sin(x- )
)
(1)求函数f(x)在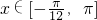 时的值域;
时的值域;
(2)求函数f(x)在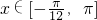 时的单调区间.
时的单调区间.
解:∵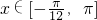 ,∴x-
,∴x- ∈
∈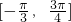
(1)∵当x= 时,x-
时,x- =
=
∴当x= 时,函数f(x)=2sin(x-
时,函数f(x)=2sin(x- )有最大值为2
)有最大值为2
∵f(- )=2sin(-
)=2sin(- )=-
)=- ,f(π)=2sin
,f(π)=2sin =
=
∴函数f(x)在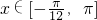 时的最小值为f(-
时的最小值为f(- )=-
)=- ,
,
综上所述,可得函数f(x)在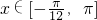 时的值域为[-
时的值域为[- ,2];
,2];
(2)∵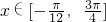 时,t=x-
时,t=x- ∈[-
∈[- ,
, ],y=sint在[-
],y=sint在[- ,
, ]是关于t的增函数,
]是关于t的增函数,
∴f(x)在区间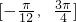 上是增函数
上是增函数
而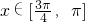 时,t=x-
时,t=x- ∈[
∈[ ,
, ],y=sint在[
],y=sint在[ ,
, ]是关于t的减函数,
]是关于t的减函数,
∴f(x)在区间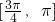 上是减函数.
上是减函数.
分析:(1)当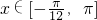 时,x-
时,x- ∈
∈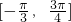 .结合正弦函数的图象与性质,可得当x=
.结合正弦函数的图象与性质,可得当x= 时,函数f(x)的最大值为2,当x=-
时,函数f(x)的最大值为2,当x=- 时有最小值为-
时有最小值为- ,由此即可得到函数f(x)在
,由此即可得到函数f(x)在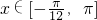 时的值域;
时的值域;
(2)令t=x- ,根据已知条件得t∈[-
,根据已知条件得t∈[- ,
, ],结合y=sint在∈[-
],结合y=sint在∈[- ,
, ]上的单调区间,即可得到f(x)在区间
]上的单调区间,即可得到f(x)在区间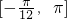 上的单调性,得到本题答案.
上的单调性,得到本题答案.
点评:本题给出三角函数f(x)=2sin(x- ),求函数在区间
),求函数在区间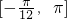 上的单调性与值域.着重考查了正弦函数的图象与性质的知识,属于基础题.
上的单调性与值域.着重考查了正弦函数的图象与性质的知识,属于基础题.
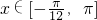 ,∴x-
,∴x- ∈
∈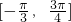
(1)∵当x=
 时,x-
时,x- =
=
∴当x=
 时,函数f(x)=2sin(x-
时,函数f(x)=2sin(x- )有最大值为2
)有最大值为2∵f(-
 )=2sin(-
)=2sin(- )=-
)=- ,f(π)=2sin
,f(π)=2sin =
=
∴函数f(x)在
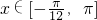 时的最小值为f(-
时的最小值为f(- )=-
)=- ,
,综上所述,可得函数f(x)在
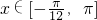 时的值域为[-
时的值域为[- ,2];
,2];(2)∵
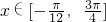 时,t=x-
时,t=x- ∈[-
∈[- ,
, ],y=sint在[-
],y=sint在[- ,
, ]是关于t的增函数,
]是关于t的增函数,∴f(x)在区间
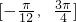 上是增函数
上是增函数而
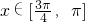 时,t=x-
时,t=x- ∈[
∈[ ,
, ],y=sint在[
],y=sint在[ ,
, ]是关于t的减函数,
]是关于t的减函数,∴f(x)在区间
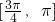 上是减函数.
上是减函数.分析:(1)当
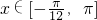 时,x-
时,x- ∈
∈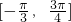 .结合正弦函数的图象与性质,可得当x=
.结合正弦函数的图象与性质,可得当x= 时,函数f(x)的最大值为2,当x=-
时,函数f(x)的最大值为2,当x=- 时有最小值为-
时有最小值为- ,由此即可得到函数f(x)在
,由此即可得到函数f(x)在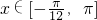 时的值域;
时的值域;(2)令t=x-
 ,根据已知条件得t∈[-
,根据已知条件得t∈[- ,
, ],结合y=sint在∈[-
],结合y=sint在∈[- ,
, ]上的单调区间,即可得到f(x)在区间
]上的单调区间,即可得到f(x)在区间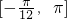 上的单调性,得到本题答案.
上的单调性,得到本题答案.点评:本题给出三角函数f(x)=2sin(x-
 ),求函数在区间
),求函数在区间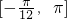 上的单调性与值域.着重考查了正弦函数的图象与性质的知识,属于基础题.
上的单调性与值域.着重考查了正弦函数的图象与性质的知识,属于基础题. 
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目