题目内容
【题目】已知a<﹣1,函数f(x)=|x3﹣1|+x3+ax(x∈R).
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)已知存在实数m,n(m<n≤1),对任意t0∈(m,n),总存在两个不同的t1 , t2∈(1,+∞),
使得f(t0)﹣2=f(t1)=f(t2),求证: ![]() .
.
【答案】解:(Ⅰ) ![]() ,
,
记 ![]() ,
,
则f2′(x)=6x2+a,
因为 a<﹣1则由f2′(x)=0可得x=± ![]() ,
,
(i) ![]() ,f1(x)在(﹣∞,1)上递减,
,f1(x)在(﹣∞,1)上递减,
f2(x)在[1,+∞)上递增,
所以[f(x)]min=f(1)=a+1;
(ii) ![]() ,f1(x)在(﹣∞,1)上递减,
,f1(x)在(﹣∞,1)上递减,  ,
,
所以  .
.
综上, 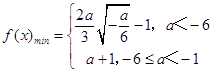 ;
;
(Ⅱ)证明:不妨设t1<t2,则由(1)知,若﹣6≤a<﹣1,则f2(x)在(1,+∞)上递增,
不满足题意,所以a<﹣6.
所以 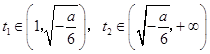 ,且
,且  ,
,
(i)a+1﹣2> ![]() ,即
,即 
即 ![]() ,解得
,解得 ![]() ,即
,即 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ;
;
(ii)a+1﹣2≤ ![]() ,即
,即 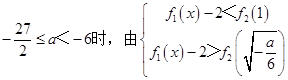 ,
,
即 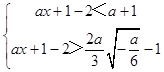 ,解得
,解得 ![]() ,
,
所以 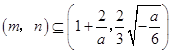 ,所以m≥1+
,所以m≥1+ ![]() ,n≤
,n≤ ![]() ,
,
所以n﹣m≤ ![]() ﹣1﹣
﹣1﹣ ![]()
令 ![]() =u∈(1,
=u∈(1, ![]() ],则
],则 ![]() ﹣1﹣
﹣1﹣ ![]() =
= ![]() u﹣1+
u﹣1+ ![]() ,
,
令φ(u)= ![]() u﹣1+
u﹣1+ ![]() ,则
,则 ![]() ,
,
所以φ(u)= ![]() u﹣1+
u﹣1+ ![]() 在u∈(1,
在u∈(1, ![]() ]递增,
]递增,
所以φ(u)≤φ( ![]() )=
)= ![]() ,所以n﹣m≤φ(u)≤
,所以n﹣m≤φ(u)≤ ![]()
【解析】(Ⅰ)运用分段函数的形式写出f(x),讨论 ![]() ,
, ![]() ,判断单调性,即可得到所求最小值;(Ⅱ)不妨设t1<t2,则由(1)知,若﹣6≤a<﹣1,则f2(x)在(1,+∞)上递增,不满足题意,所以a<﹣6.讨论(i)a+1﹣2>
,判断单调性,即可得到所求最小值;(Ⅱ)不妨设t1<t2,则由(1)知,若﹣6≤a<﹣1,则f2(x)在(1,+∞)上递增,不满足题意,所以a<﹣6.讨论(i)a+1﹣2> ![]() ,(ii)a+1﹣2≤
,(ii)a+1﹣2≤ ![]() ,运用不等式的性质,求出n﹣m的不等式,即可得到证明.
,运用不等式的性质,求出n﹣m的不等式,即可得到证明.
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数).现随机抽取20天的指数(见下表),将指数不低于8.5视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(Ⅱ)以这20天的数据估计我市总体空气质量(天数很多).若从我市总体空气质量指数中随机抽取3天的指数,用X表示抽到空气质量为优良的天数,求X的分布列及数学期望.
