Question

（2012•韶关一模）已知函数f（x）=ax³+bx²+（b-a）x（a，b是不同时为零的常数），其导函数为f'（x）．
（1）当a=

1

3

时，若不等式f′(x)＞-

1

3

对任意x∈R恒成立，求b的取值范围；
（2）若函数f（x）为奇函数，且在x=1处的切线垂直于直线x+2y-3=0，关于x的方程f(x)=-

1

4

t在[-1，t]（t＞-1）上有且只有一个实数根，求实数t的取值范围．

Answer 1

分析：（1）求导函数，将不等式f′(x)＞-

1

3

对任意x∈R恒成立，转化为x²+2bx+b＞0恒成立，利用判别式，即可确定b的取值范围；
（2）先确定函数的解析式，确定f（x）的单调性，由f（x）=0解得x=±1，x=0；
法一：作y=f（x）与y=-

t

4

的图象，若只有一个交点，结合图象分类讨论；
法二：作y=f（x）与y=-

1

4

x的图知交点横坐标为x=±

3

2

，x=0，当x∈[-

3

2

，0)∪(0，

3

2

)∪{

8 3

9

}时，过y=-

1

4

x图象上任意一点向左作平行于x轴的直线与y=f（x）都只有唯一交点，当x取其它任何值时都有两个或没有交点，由此可得结论．

解答：解：（1）当a=

1

3

时，f′(x)=x2+2bx+b-

1

3

，…（1分）
依题意　f′(x)=x2+2bx+b-

1

3

＞-

1

3

即x²+2bx+b＞0恒成立
∴△=4b²-4b＜0，解得　0＜b＜1
所以b的取值范围是（0，1）…（4分）
（2）因为f（x）=ax³+bx²+（b-a）x为奇函数，所以b=0，所以f（x）=ax³-ax，f'（x）=3ax²-a．
又f（x）在x=1处的切线垂直于直线x+2y-3=0，所以a=1，即f（x）=x³-x．…（6分）
∴f（x）在(-∞，-

3

3

)，(

3

3

，+∞)上是单调递增函数，在[-

3

3

，

3

3

]上是单调递减函数，
由f（x）=0解得x=±1，x=0，…（7分）
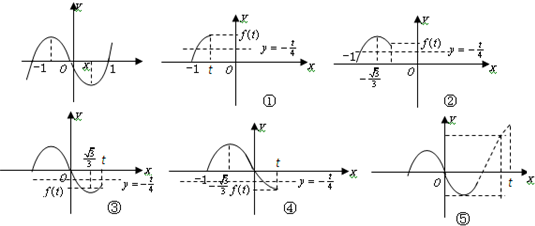
法一：如图所示，作y=f（x）与y=-

t

4

的图象，若只有一个交点，则
①当-1＜t≤-

3

3

时，f(t)≥-

1

4

t≥0，即t3-t≥-

t

4

，解得-

3

2

≤t≤-

3

3

；
②当-

3

3

＜t＜0时，f(t)＞-

1

4

t≥0，解得-

3

3

＜t＜0；③当t=0时，不成立；
④当0＜t≤

3

3

时，f(t)≤-

1

4

t＜0，即t3-t≤-

t

4

，解得0＜t≤

3

3

；
⑤当1≥t＞

3

3

时，f(t)＜-

1

4

t＜0，解得

3

3

＜t＜

3

2

；
⑥当t＞1时，1-

t

4

=f(

3

3

)⇒t=

8 3

9

.y=-

t

4

…（13分）
综上t的取值范围是-

3

2

≤t＜0或0＜t＜

3

2

或t=

8 3

9

．…（14分）
法二：作y=f（x）与y=-

1

4

x的图知交点横坐标为x=±

3

2

，x=0
当x∈[-

3

2

，0)∪(0，

3

2

)∪{

8 3

9

}时，过y=-

1

4

x图象上任意一点向左作平行于x轴的直线与y=f（x）都只有唯一交点，当x取其它任何值时都有两个或没有交点．
所以当t∈[-

3

2

，0)∪(0，

3

2

)∪{

8 3

9

}时，方程f(x)=-

1

4

t在[-1，t]（t＞-1）上有且只有一个实数根．

点评：本题考查导数知识的运用，考查恒成立问题，考查数形结合的数学思想，考查分类讨论的数学思想，属于中档题．