题目内容

函数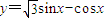，的值域是    ．
【答案】分析：根据两角和与差的正弦公式可得：y=2sin（x-），再根据题意可得x+，然后利用正弦函数的图象可得-≤sin（x-）≤，进而得到答案．
解答：解：由题意可得：y=sinx-cosx=2sin（x-），
因为，
所以x+，
所以-≤sin（x-）≤，
所以-≤y≤1．
故答案为：[-，1]．
点评：本题主要考查了正弦函数的有关性质，即值域与定义域．解题的关键是利用两角和与差的正弦余弦该点对函数解析式进行正确化简，以及对正弦函数的性质的熟练运用．
练习册系列答案
相关题目
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
C
x
n
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数
C
x
8
的值域是（　　）
A、[
16
3
，28]
B、[
16
3
，56)
C、(4，
28
3
)∪[28，56）
D、(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数，如[2]=2，[
5
4
]=1，对于给定的n∈N*，定义Cnx=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则C
3
28
=
 
；当x∈[2，3）时，函数Cx8的值域是
 
．
给出下列四个判断：
①定义在R上的奇函数f（x），当x＞0时f（x）=x2+2，则函数f（x）的值域为{y|y≥2或y≤-2}；
②若不等式x3+x2+a＜0对一切x∈[0，2]恒成立，则实数a的取值范围是{a|a＜-12}；
③当f（x）=log3x时，对于函数f（x）定义域中任意的x1，x2（x1≠x2）都有f(
x1+x2
2
)＜
f(x1)+f(x2)
2
；
④设g（x）表示不超过t＞0的最大整数，如：[2]=2，[1.25]=1，对于给定的n∈N+，定义
C
x
n
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，2）时函数
C
x
8
的值域是(4，
16
3
]；
上述判断中正确的结论的序号是
②④
②④
．
设[x]表示不超x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
C
x
n
=
n(n-1)(n-2)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞)，则 （i）
C
3
2
8
=
16
3
16
3
；（ii）当x∈[2，3）时，函数
C
x
8
的值域是
(
28
3
，28]
(
28
3
，28]
．
函数y=的值域是________________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网