Question

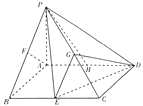
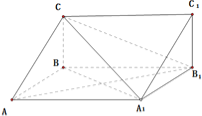
【题目】【2017安徽淮北二模】如图，三棱柱中，四边形是菱形，,二面角为， .

（Ⅰ）求证：平面平面;

（Ⅱ）求二面角的余弦值.

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）先由三棱柱性质将线面垂直转化为，再由得线线垂直，又由是菱形得,最后根据线面垂直判定定理得线面垂直, 根据面面垂直判定定理得平面平面.（2）求二面角的大小，一般借助空间向量数量积求解，先根据条件建立空间直角坐标系，设立各点坐标，利用方程组解出各面法向量，利用向量数量积求两法向量夹角，最后根据二面角与法向量夹角关系求二面角.

试题解析：（1）证明：在三棱柱中，由

得，则，

又是菱形, 得,而,

则,

故平面平面.

（2）

由题意得为正三角形，

取得中点为D，连CD,BD,

则,又

易得,则为二面角的平面角，

因, =,所以,

所以

过交点作,垂足为,连

则为二面角的平面角，

又 得

所以

另：建系用向量法相应给分。