题目内容
已知sin(a+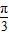 )+sina=-
)+sina=-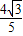 ,-
,-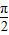 <a<0,则cos(a+
<a<0,则cos(a+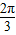 )等于 .
)等于 .
【答案】分析:将已知等式的左边利用两角和与差的正弦函数公式化简,合并后提取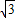 ,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(α+
,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(α+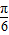 )的值,将α+
)的值,将α+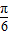 变形为
变形为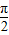 +(α-
+(α-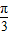 ),利用诱导公式化简,求出cos(α-
),利用诱导公式化简,求出cos(α-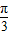 )的值,然后将所求式子中的角α+
)的值,然后将所求式子中的角α+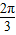 变形为π+(α-
变形为π+(α-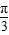 ),利用诱导公式化简后,将cos(α-
),利用诱导公式化简后,将cos(α-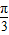 )的值代入即可求出值.
)的值代入即可求出值.
解答:解:∵sin(α+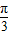 )+sinα=
)+sinα= sinα+
sinα+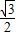 cosα+sinα
cosα+sinα
= sinα+
sinα+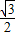 cosα=
cosα=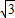 (
(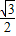 sinα+
sinα+ cosα)=
cosα)=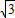 sin(α+
sin(α+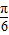 )=-
)=-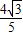 ,
,
∴sin(α+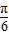 )=sin[
)=sin[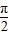 +(α-
+(α-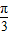 )]=cos(α-
)]=cos(α-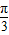 )=-
)=- ,
,
则cos(α+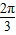 )=cos[π+(α-
)=cos[π+(α-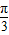 )]=-cos(α-
)]=-cos(α-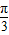 )=
)= .
.
故答案为:
点评:此题考查了两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,灵活变换角度,熟练掌握公式是解本题的关键.
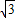 ,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(α+
,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(α+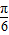 )的值,将α+
)的值,将α+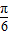 变形为
变形为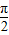 +(α-
+(α-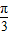 ),利用诱导公式化简,求出cos(α-
),利用诱导公式化简,求出cos(α-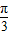 )的值,然后将所求式子中的角α+
)的值,然后将所求式子中的角α+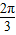 变形为π+(α-
变形为π+(α-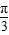 ),利用诱导公式化简后,将cos(α-
),利用诱导公式化简后,将cos(α-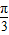 )的值代入即可求出值.
)的值代入即可求出值.解答:解:∵sin(α+
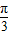 )+sinα=
)+sinα= sinα+
sinα+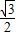 cosα+sinα
cosα+sinα=
 sinα+
sinα+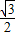 cosα=
cosα=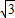 (
(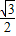 sinα+
sinα+ cosα)=
cosα)=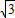 sin(α+
sin(α+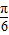 )=-
)=-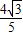 ,
,∴sin(α+
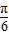 )=sin[
)=sin[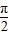 +(α-
+(α-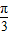 )]=cos(α-
)]=cos(α-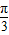 )=-
)=- ,
,则cos(α+
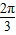 )=cos[π+(α-
)=cos[π+(α-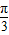 )]=-cos(α-
)]=-cos(α-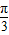 )=
)= .
.故答案为:

点评:此题考查了两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,灵活变换角度,熟练掌握公式是解本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知sin(π+a)=
且a是第三象限的角,则cos(2π-a)的值是( )
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|