题目内容
已知a≠0,b≠0,且a
证明:令a=(x1,y1),b=(x2,y2),
a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2),
假设a+b∥a-b,
则(x1+x2)(y1-y2)-(y1+y2)(x1-x2)=0,
即x1y1+x2y1-x1y2-x2y2-x1y1-x1y2+x2y1+x2y2=0,
整理得2(x2y1-x1y2)=0,即x1y2-x2y1=0,
因为a≠0,b≠0,所以a∥b.
这与已知矛盾,故a+b与a-b不平行.
温馨提示
平面向量的坐标表示,将几何问题转化为代数问题,通过向量的代数运算使几何问题得到解决,这是数形结合思想的体现.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
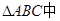 ,已知A(-
,已知A(-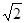 ,0),
B(
,0),
B(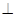 AB于D,
AB于D, 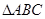 的垂心为H,且
的垂心为H,且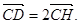

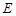 于不同的两点
于不同的两点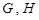 (点
(点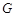 在F,H之间),且满足
在F,H之间),且满足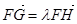 ,求
,求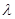 的取值范围.
的取值范围.