题目内容
 一个几何体的三视图如图所示.
一个几何体的三视图如图所示.(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积;
(Ⅲ)设异面直线AA'与BC'所成的角为θ,求cosθ.
分析:(Ⅰ)根据几何体的三视图判断该几何体的形状,就可画出直观图.
(Ⅱ)由几何体的三视图可判断这个几何体是直三棱柱,所以体积是底面积乘高.根据三视图中所给数据,就可求出底面三角形的面积和高,进而求出体积.
(Ⅲ)因为AA'∥BB',所以AA'与BC'所成的角是∠B'BC',然后在三角形BB'C'中计算此角的余弦值即可
(Ⅱ)由几何体的三视图可判断这个几何体是直三棱柱,所以体积是底面积乘高.根据三视图中所给数据,就可求出底面三角形的面积和高,进而求出体积.
(Ⅲ)因为AA'∥BB',所以AA'与BC'所成的角是∠B'BC',然后在三角形BB'C'中计算此角的余弦值即可
解答:解:(Ⅰ)这个几何体的直观图如图所示
(Ⅱ)这个几何体是直三棱柱.
由于底面△ABC的高为1,所以AC=BC=
=
,
BB′=CC′=AA′=3
故所求全面积S=2S△ABC+2SBB'C'C+SABB′A′=2×
×2×1+3×2+2×3×
=8+6
(cm2)
(Ⅲ)因为AA'∥BB',所以AA'与BC'所成的角是∠B'BC'.
在Rt△BB'C'中,BC′=
=
=
,
故cosθ=
=
=

(Ⅱ)这个几何体是直三棱柱.
由于底面△ABC的高为1,所以AC=BC=
| 12+12 |
| 2 |
BB′=CC′=AA′=3
故所求全面积S=2S△ABC+2SBB'C'C+SABB′A′=2×
| 1 |
| 2 |
| 2 |
| 2 |
(Ⅲ)因为AA'∥BB',所以AA'与BC'所成的角是∠B'BC'.
在Rt△BB'C'中,BC′=
| BB′2+B′C′2 |
| 32+22 |
| 13 |
故cosθ=
| BB′ |
| BC′ |
| 3 | ||
|
| 3 |
| 13 |
| 13 |
点评:本题考察了三视图、直观图的特点及其画法,直三棱柱体积的计算,空间线线角的求法,需要有较强的空间想象力

练习册系列答案
相关题目
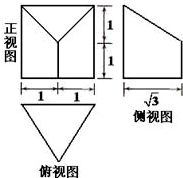
 (2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )
(2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )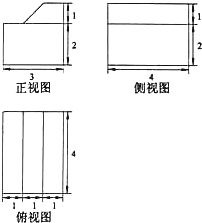 (2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为
(2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为 (2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为
(2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为