题目内容
若 是常数,函数
是常数,函数 对于任何的非零实数
对于任何的非零实数 都有
都有 ,且
,且 ,则不等式
,则不等式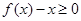 的解集为( )
的解集为( )
A.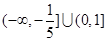 | B.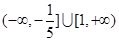 |
C.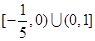 | D.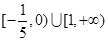 |
A
解析试题分析:根据题意可知,
令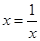 ,则原式变形为
,则原式变形为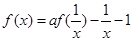 ,那么联立方程组消去
,那么联立方程组消去 ,得到
,得到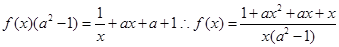
那么由于f(1)=1,可知a=3,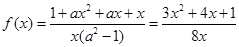 ,那么解一元二次不等式可知
,那么解一元二次不等式可知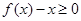 的解集为
的解集为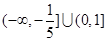 ,选A.
,选A.
考点:本试题考查了函数与不等式的关系运用。
点评:解决不等式的解集问题,要结合函数的解析式,以及一元二次不等式的解法来得到,那么求解函数的解析式是关键,运用联立方程组的思想来得到结论,属于中档题。

练习册系列答案
相关题目
已知集合 ,则
,则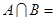 ( )
( )
A. | B.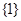 | C.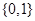 | D.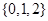 |
集合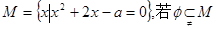 ,则实数
,则实数 的取值范围是
的取值范围是
A.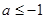 | B.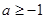 | C.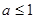 | D.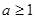 |
设全集 ,
,
 则
则 ( )
( )
A. | B. | C.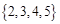 | D. |
设集合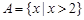 ,则( )
,则( )
A.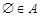 | B.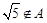 | C.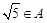 | D.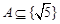 |
若集合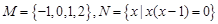 ,则
,则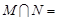
A. | B.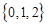 | C.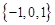 | D.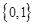 |
设集合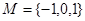 ,
, ,则
,则 ( )
( )
A.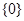 | B.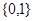 | C.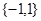 | D.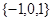 |
集合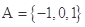 ,
, ,则
,则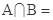 ( )
( )
| A.{0} | B.{1} | C.{0,1} | D.{-1,0,1} |
若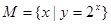 ,
, 则
则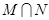 = ( )
= ( )
A.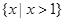 | B.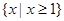 | C.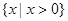 | D. R |