题目内容
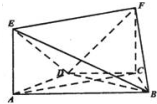 (2013•枣庄一模)如图所示的几何体中,ABCD是等腰梯形,AB∥CD,ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=CF=a,∠ACB=
(2013•枣庄一模)如图所示的几何体中,ABCD是等腰梯形,AB∥CD,ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=CF=a,∠ACB=| π | 2 |
(1)若M∈EF,AM∥平面BDF,求EM的长度;
(2)求二面角B-EF-C的平面角θ的大小.
分析:(1)设AC∩BD=0,连结OF,利用平行线的性质结合等腰梯形的性质,证出∠CB0=∠DAC=
∠CBA,结合∠ACB=90°利用三角形内角和定理,算出∠CB0=30°,从而Rt△OCB中算出OC=BCtan30°=
a.由线面平行的性质定理证出AM∥OF,结合矩形ACFE中AC=EF,可得EM=OC=
a;
(2)以C为原点,CA、CB、CF所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.得到B、C、E、F各点的坐标,从而得到向量
、
的坐标,利用垂直向量数量积为0的方法建立方程组,解出
=(0,1,1)为平面BEF的一个法向量,结合平面EFC的一个法向量为
=(0,1,0),利用空间向量的夹角公式即可算出二面角B-EF-C的平面角θ的大小.
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
(2)以C为原点,CA、CB、CF所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.得到B、C、E、F各点的坐标,从而得到向量
| BF |
| BE |
| m |
| n |
解答:解:(1)设AC∩BD=0,连结OF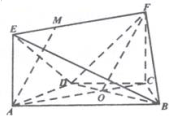
∵等腰梯形ABCD中,DA=DC,∴∠DAC=∠DCA
∵AB∥CD,∴∠CAB=∠DCA,可得∠DAC=∠CAB.同理可证∠CB0=∠AB0
∵等腰梯形ABCD中,∠DAB=∠CBA,∴∠CB0=∠DAC=
∠CBA
又∵∠DCA+∠ACB+∠CBA=180°,∠ACB=90°
∴3∠CB0=90°,得∠CB0=30°
Rt△OCB中,BC=a,可得OC=BCtan30°=
a
∵AM∥平面BDF,AM?平面ACEF,平面BDF∩平面ACEF=OF,∴AM∥OF
∵四边形ACFE是矩形,可得AC=EF,∴EM=OC=
a;
(2)以C为原点,CA、CB、CF所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图所示.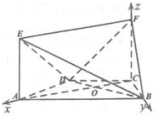
可得C(0,0,0),B(0,a,0),F(0,0,a),E(
a,0,a),
设平面BEF的一个法向量为
=(x,y,z),可得
,
取y=1,得x=0,z=1,可得
=(0,1,1)为平面BEF的一个法向量.
∵平面EFC的一个法向量为
=(0,1,0),且cos<
,
>=
=
∴二面角B-EF-C的平面角θ满足|cosθ|=
,
结合二面角B-EF-C是一个锐二面角,可得θ=45°.

∵等腰梯形ABCD中,DA=DC,∴∠DAC=∠DCA
∵AB∥CD,∴∠CAB=∠DCA,可得∠DAC=∠CAB.同理可证∠CB0=∠AB0
∵等腰梯形ABCD中,∠DAB=∠CBA,∴∠CB0=∠DAC=
| 1 |
| 2 |
又∵∠DCA+∠ACB+∠CBA=180°,∠ACB=90°
∴3∠CB0=90°,得∠CB0=30°
Rt△OCB中,BC=a,可得OC=BCtan30°=
| ||
| 3 |
∵AM∥平面BDF,AM?平面ACEF,平面BDF∩平面ACEF=OF,∴AM∥OF
∵四边形ACFE是矩形,可得AC=EF,∴EM=OC=
| ||
| 3 |
(2)以C为原点,CA、CB、CF所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图所示.

可得C(0,0,0),B(0,a,0),F(0,0,a),E(
| 3 |
设平面BEF的一个法向量为
| m |
|
取y=1,得x=0,z=1,可得
| m |
∵平面EFC的一个法向量为
| n |
| m |
| n |
| ||||
|
|
| ||
| 2 |
∴二面角B-EF-C的平面角θ满足|cosθ|=
| ||
| 2 |
结合二面角B-EF-C是一个锐二面角,可得θ=45°.
点评:本题给出底面为等腰梯形且一个侧面与底面垂直的多面体,求二面角的大小.着重考查了线面平行的性质定理、等腰梯形的性质和利用空间向量求二面角的大小等知识,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目