题目内容
．已知命题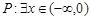
，
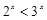；命题
，
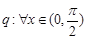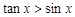．则下列命题命题为真的是 （ ）
A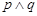． | B． |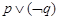
C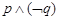． | D． |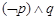
D
解析考点：复合命题的真假．
分析：由指数函数的性质，我们易判断命题p的真假，根据三角函数的性质，我们易判断命题q的真假，然后根据复合命题真假判断的“真值表”我们易得正确答案．
解：因为当x＜0时，(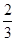
)x＞1，
即2x＞3x，所以命题p为假，从而﹁p为真．
因为当x∈(0，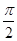
)时，tanx-sinx=
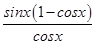＞0，
即tanx＞sinx，所以命题q为真．
所以（﹁p）∧q为真，
故选D．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、命题：“已知函数f（x），若f（x+1）与f（x-1）均为奇函数，则f（x）为奇函数，”为直命题 | B、“x＞1”是“|x|＞1”的必要不充分条件 | C、若“p且q”为假命题，则p，q均为假命题 | D、命题p：”?x∈R，使得x2+x+1＜0”，则?p：”?x∈R，均有x2+x+1≥0” |
已知命题p：?x∈R，使sinx=
；命题q：?x∈R，都有x2+x+1＞0．下列结论中正确的（ ）
| ||
| 2 |
| A、命题“p∧q”是真命题 |
| B、命题“p∧非q”是真命题 |
| C、命题“非p∧q”是真命题 |
| D、命题“非p∧q”是假命题 |