题目内容
已知函数f(x)=2sinxcosx-2cos2x(x∈R).
(1)求函数f(x)的对称轴方程;
(2)当 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
解:(1)因为f(x)=2sinxcosx-2cos2x=sin2x-cos2x-1= ,
,
令 k∈Z),即f(x)的对称轴方程为
k∈Z),即f(x)的对称轴方程为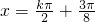 (k∈Z).…(6分)
(k∈Z).…(6分)
(2) .
.
当 时,
时, ,所以当
,所以当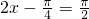 ,即
,即 时,
时, ; …(10分)
; …(10分)
当 ,即x=0时,f(x)min=-2,
,即x=0时,f(x)min=-2,
故函数f(x)的取值范围是 .…(12分)
.…(12分)
分析:(1)利用二倍角公式、辅助角公式化简函数,利用正弦函数的性质,可得函数f(x)的对称轴方程;
(2)整体思维,求得角的范围,利用正弦函数的性质,可得函数f(x)的取值范围.
点评:本题考查三角恒等变换,考查三角函数的性质,解题的关键是正确化简函数.
 ,
,令
 k∈Z),即f(x)的对称轴方程为
k∈Z),即f(x)的对称轴方程为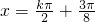 (k∈Z).…(6分)
(k∈Z).…(6分)(2)
 .
.当
 时,
时, ,所以当
,所以当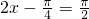 ,即
,即 时,
时, ; …(10分)
; …(10分)当
 ,即x=0时,f(x)min=-2,
,即x=0时,f(x)min=-2,故函数f(x)的取值范围是
 .…(12分)
.…(12分)分析:(1)利用二倍角公式、辅助角公式化简函数,利用正弦函数的性质,可得函数f(x)的对称轴方程;
(2)整体思维,求得角的范围,利用正弦函数的性质,可得函数f(x)的取值范围.
点评:本题考查三角恒等变换,考查三角函数的性质,解题的关键是正确化简函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目