��Ŀ����
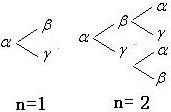 �æ����£���������ĸ���һ������Ϊn+1��n��N*������ĸ���ַ�����Ҫ���ɦ���ʼ������������ĸ��ͬ������n=1ʱ���ų����ַ��������Ǧ��»���ã�n=2ʱ�ų����ַ��������Ǧ��¦������¦ã����æ������æ£���ͼ������������n+1���ַ����У��������һ������ĸ���Ǧ��������ַ���������Ϊan����֪��a1=0��a2=2����a4=
�æ����£���������ĸ���һ������Ϊn+1��n��N*������ĸ���ַ�����Ҫ���ɦ���ʼ������������ĸ��ͬ������n=1ʱ���ų����ַ��������Ǧ��»���ã�n=2ʱ�ų����ַ��������Ǧ��¦������¦ã����æ������æ£���ͼ������������n+1���ַ����У��������һ������ĸ���Ǧ��������ַ���������Ϊan����֪��a1=0��a2=2����a4=�����������ƹ�ʽΪan+1=pan+qn������ת��
=
+
����ת����an+1-t=s��an-t���������û�Ԫ��ת��Ϊ�ȱ�������⣮
| an+1 |
| qn+1 |
| p |
| q |
| an |
| qn |
| 1 |
| q |
����⣺������ͼ��an+1=2n-an
��
=-
•
+
��
-
=-
•��
-
��
��
-
=��-
��•(-
)n-1
��an=
•2n-
•(-1)n-1
������{an}��ǰ2n��֮��a1+a2+a3+��+a2n=
(2+22+23+��+22n)-
(1-1+1-1+��+1-1)
=
(2+22+23+��+22n)=
(22n-1)=
�ʴ�Ϊ��
��
| an+1 |
| 2n+1 |
| 1 |
| 2 |
| an |
| 2n |
| 1 |
| 2 |
��
| an+1 |
| 2n+1 |
| 1 |
| 3 |
| 1 |
| 2 |
| an |
| 2n |
| 1 |
| 3 |
��
| an |
| 2n |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
��an=
| 1 |
| 3 |
| 2 |
| 3 |
������{an}��ǰ2n��֮��a1+a2+a3+��+a2n=
| 1 |
| 3 |
| 2 |
| 3 |
=
| 1 |
| 3 |
| 2 |
| 3 |
| 2(4n-1) |
| 3 |
�ʴ�Ϊ��
| 2(4n-1) |
| 3 |
���������ô���ϵ����������Ȳ�ȱ�������ͨ�

��ϰ��ϵ�д�
�����Ŀ