题目内容
请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示)。试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?

解:设OO1为xm,则
设题设可得正六棱锥底面边长为(单位:m)
于是底面正六边形的面积为(单位:m2)
帐篷的体积为(单位:m3)
求导数,得
令 ,解得
,解得 (不合题意,舍去),x=2
(不合题意,舍去),x=2
当 时,
时, ,
, 为增函数
为增函数
当 时,
时, ,
, 为减函数
为减函数
所以当x=2时,V(x)最大
答:当OO1为2m时,帐逢的体积最大。

设题设可得正六棱锥底面边长为(单位:m)

于是底面正六边形的面积为(单位:m2)

帐篷的体积为(单位:m3)

求导数,得

令
 ,解得
,解得 (不合题意,舍去),x=2
(不合题意,舍去),x=2当
 时,
时, ,
, 为增函数
为增函数当
 时,
时, ,
, 为减函数
为减函数所以当x=2时,V(x)最大
答:当OO1为2m时,帐逢的体积最大。

练习册系列答案
相关题目
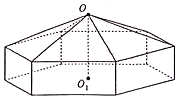 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
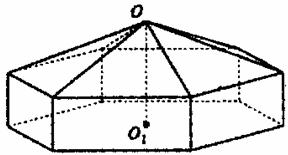
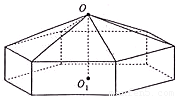 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?