题目内容
已知奇函数![]() 的图像在
的图像在![]() (1,
(1,![]() )处的切线的斜率为6.且
)处的切线的斜率为6.且![]() =2时,
=2时,![]() 取得极值.
取得极值.
(1)求实数![]() 、
、![]() 的值;
的值;
(2)设函数![]() 的导函数为
的导函数为![]() ,函数
,函数![]() 的导函数
的导函数
![]() ,
,![]() (0,1),求函数
(0,1),求函数![]() 的单调区间;
的单调区间;
(3)在(2)的条件下,当![]()
![]()
![]() 时,
时,![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围.
的取值范围.
解:(Ⅰ)∵![]() 是奇函数,
是奇函数,
由![]() 恒成立,有
恒成立,有![]() .
.
从而![]() .
.![]()
又![]() ,
,
![]()
![]()
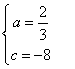 故
故![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)依题意,![]()
令![]() ,得
,得![]() 或
或![]() .
.
当![]() 变化时,
变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
|
| ( | ( | (3 |
|
| ― | + | ― |
|
| 递减 | 递增 | 递减 |
由表可知:当![]()
![]() (
(![]() ,
,![]() )时,函数
)时,函数![]() 为减函数;当
为减函数;当![]()
![]() (3
(3![]() ,+
,+![]() )时,
)时,
函数![]() 也为减函数;当
也为减函数;当![]()
![]() (
(![]() ,3
,3![]() ),函数
),函数![]() 为增函数.
为增函数.
∴函数![]() 的单调递增区间为(
的单调递增区间为(![]() ,3
,3![]() ),单调递减区间为(
),单调递减区间为(![]() ,
,![]() ),(3
),(3![]() ,+
,+![]() ).
).
(3)由![]() ,得
,得![]() .
.
∵![]() ,∴
,∴![]() .
.
![]() 在
在![]() 上为减函数.
上为减函数.
∴![]() ;
;
![]() .
.
于是,问题转化为求不等式![]() 的解.
的解.
解此不等式组,得![]() .又
.又![]() ,∴所求
,∴所求![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目


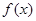 是定义在
是定义在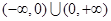 上的奇函数,当
上的奇函数,当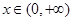 时,
时,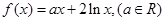
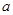 ,使得当
,使得当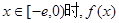 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出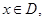 如果函数
如果函数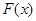 的图像在函数
的图像在函数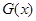 的图像的下方,则称函数
的图像的下方,则称函数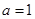 时,函数
时,函数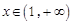 上被函数
上被函数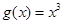 覆盖.
覆盖.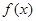 是定义在
是定义在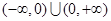 上的奇函数,当
上的奇函数,当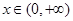 时,
时,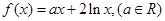
 ,使得当
,使得当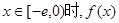 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出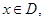 如果函数
如果函数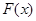 的图像在函数
的图像在函数 的图像的下方,则称函数
的图像的下方,则称函数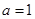 时,函数
时,函数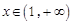 上被函数
上被函数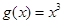 覆盖。
覆盖。