题目内容
数列{an}的前n项和Sn=100n-n2(n∈N*),______________.(先在横线上填上一个结论,然后再解答)
构建问题(一):数列{an}的前n项和Sn=100n-n2(n∈N*)
,数列{an}是什么数列?
解析:由an=Sn-Sn-1=(100n-n2)+[100(n-1)-(n-1)2]=101-2n(n≥2),
∵a1=S1=100×1-12=99=101-2×1,
∴数列{an}的通项公式为an=101-2n(n∈N*).
又∵an+1-an=-2为常数,
∴数列{an}是首项a1=99,公差d=-2的等差数列.
构建问题(二):数列{an}的前n项和Sn=100n-n2(n∈N*),求数列{|an|}的前n项和.
解析:设bn=|an|.令an=101-2n≥0,得n≤50.5.
∵n∈N*,∴ n≤50(n∈N*).
当1≤n≤50时,an>0,此时bn=|an|=an,
∴ {bn}的前n项和Sn′=100n-n2且S50′=100×50-502=2 500;
当n≥51时,an<0,此时bn=|an|=-an,
由b51+b52+…+bn=-(a51+a52+…+an)=-(Sn-S50)=S50-Sn,
得数列{bn}的前n项和为Sn′=S50+S50-Sn=2S50-Sn=2×2 500-(100n-n2)=5 000-100n+n2.
∴Sn=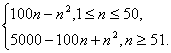

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目