题目内容
已知曲线C1的极坐标方程是ρ=
,曲线C2的参数方程是
(t>0,θ∈[
,
],θ是参数).
(1)写出曲线C1的直角坐标方程和曲线C2的普通方程;
(2)求t的取值范围,使得C1,C2没有公共点.
| 2 |
|
| π |
| 6 |
| π |
| 2 |
(1)写出曲线C1的直角坐标方程和曲线C2的普通方程;
(2)求t的取值范围,使得C1,C2没有公共点.
分析:(1)把曲线C1的极坐标方程化为直角坐标方程是x2+y2=2,把曲线C2的参数方程化为普通方程是x=1(t+
≤y≤2t+
).
(2)结合图象,根据直线和圆的位置关系可得,当且仅当
或
时,C1,C2没有公共点,由此求得t的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)结合图象,根据直线和圆的位置关系可得,当且仅当
|
|
解答:解:(1)曲线C1的直角坐标方程是x2+y2=2,表示以原点(0,0)为圆心,半径等于
的圆.
曲线C2的普通方程是x=1(t+
≤y≤2t+
),表示一条垂直于x轴的线段,包括端点. …(5分)
(2)结合图象,根据直线和圆的位置关系可得,当且仅当
或
时,C1,C2没有公共点,
解得0<t<
或t>
,即t的取值范围为 (0,
)∪(
,+∞).…(10分)
| 2 |

曲线C2的普通方程是x=1(t+
| 1 |
| 2 |
| 1 |
| 2 |
(2)结合图象,根据直线和圆的位置关系可得,当且仅当
|
|
解得0<t<
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查把参数方程化为普通方程、把极坐标方程化为直角坐标方程的方法,直线和圆的位置关系的应用,属于基础题.

练习册系列答案
相关题目
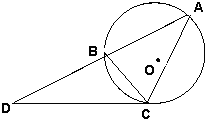 (1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,
(1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,