题目内容

6．已知f1（x）=sinx，fn（x）=f′n-1（x），n≥2，则$\sum_{i=1}^{2008}{{f_i}（0）=}$0．

分析 求函数的导数，得到得fn+4（x）=fn（x），利用函数的周期性进而可求出答案

解答 解：∵（sinx）′=cosx，（cosx）′=-sinx，（-sinx）′=-cosx，（-cosx）′=sinx，
∴fn+4（x）=fn（x），n∈N*，
即函数fn（x）是周期为4的周期函数，
且f1（x）+f2（x）+f3（x）+f4（x）=sinx+cosx-sinx-cosx=0，
则$\sum_{i=1}^{2008}{{f_i}（0）=}$502（f1（x）+f2（x）+f3（x）+f4（x））=502×0=0，
故答案为：0

点评 本题考查了三角函数的导数，理解三角函数的导函数具有周期性是解决此问题的关键．

练习册系列答案
相关题目
16．已知数列{an}的首项为a1=1，且其前n项和Sn满足Sn+1=Sn+4n+1，n∈N*．
（1）求Sn的表达式，并令bn=$\frac{{S}_{n}}{n+p}$．求非零常数p的值，使得数列{bn}是等差数列；
（2）在（1）的条件下，设cn=$\frac{1}{{b}_{n}{b}_{n+1}}$．Tn是数列{cn}的前n项和，且Tn＜m时对所有n∈N*都成立，求实数m的取值范围．
17．在△ABC中，角A、B、C所对的边分别为a、b、c，且a=4$\sqrt{2}$，b=4$\sqrt{3}$，A=45°，求角B的大小．
14．角α的终边上有一点（1，-2），则sinα=（　　）
A．-$\frac{{\sqrt{5}}}{5}$B．-$\frac{2}{5}\sqrt{5}$C．$\frac{{\sqrt{5}}}{5}$D．$\frac{2}{5}\sqrt{5}$
1．已知以点A（-1，2）为圆心的圆与直线m：x+2y+7=0相切，过点B（-2，0）的动直线l与圆A相交于M、N两点
（1）求圆A的方程．
（2）当|MN|=2$\sqrt{19}$时，求直线l方程．
11．“直线l垂直于△ABC的边AB，AC”是“直线l垂直于△ABC的边BC”的（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分也非必要条件
18．定义：若两椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1，{C_2}：\frac{x^2}{{{a_2}^2}}+\frac{y^2}{{{b_2}^2}}$=1满足$\frac{a_2}{a_1}=\frac{b_2}{b_1}$=λ，则称椭圆C1与椭圆C2相似，相似比为λ，现有一系列相似椭圆Cn：$\frac{x^2}{{{a_n}^2}}+\frac{y^2}{{{b_n}^2}}$=1，满足a1=$\sqrt{2}$，b1=1，相似比λ=2，直线l：y=x与这一系列相似椭圆在第一象限内的交点分别为A1，A2，…，An，设αn=|AnAn+1|．
（1）求α1；
（2）求证：{an}为等比数列，并求出其通项公式；
（3）令${β_n}={log_2}（\sqrt{3}{α_n}）$，求证$\frac{β_1}{β_2}+\frac{{{β_1}•{β_3}}}{{{β_2}•{β_4}}}+…+\frac{{{β_1}•{β_3}•{β_5}…{β_{2n-1}}}}{{{β_2}•{β_4}•{β_6}…{β_{2n}}}}＜\sqrt{2{β_n}+1}$-1．
15．已知g（x）=a0+a1x+a2x2+…+a10x10，h（x）=b0+b1x+b2x2+…+b9x9，若（1+x）（1-2x）19 =
（1-x）10g（x）+h（x），则a9=（　　）
A．0B．10×219C．-10×218D．-3×218
16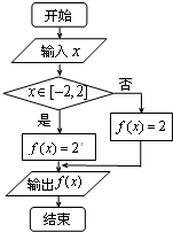．阅读程序框图，如果输出的函数值在区间[2，4]内，则输入的实数x的取值范围是（　　）
A．（-∞，-2]B．（-∞，-2）C．[1，+∞）D．（-∞，-2）∪[1，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网