题目内容

已知二次函数f（x）=ax²+bx+a满足条件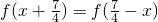 $数学公式$ ，且方程f（x）=7x+a有两个相等的实根．
（1）求f（x）的解析式；
（2）是否存在实数m，n（0＜m＜n），使f（x）的定义域和值域分别是 $数学公式$ ？若存在，求出m，n的值；若不存在，请说明理由．

解：（1）因为二次函数f（x）=ax²+bx+a满足条件 $\text{[math]}$ ，
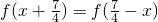所以f（x）=ax²+bx+a= $\text{[math]}$ ，
∴ $\text{[math]}$
又因为方程f（x）=7x+a有连个相等的实数根，即 $\text{[math]}$ 有两个相等的实数根．
所以△= $\text{[math]}$ -4a•0=0，
解得a=-2，
∴b=7
故f（x）=-2x²+7x-2．…（（6分））
（2）存在．如图所示：
设 $\text{[math]}$ （x＞0），则当f（x）=g（x）时，即 $\text{[math]}$
化简得：2x³-7x²+2x+3=0，故（x-3）（2x²-x-1）=0，
解得：x₁=1，x₂=3，x₃= $\text{[math]}$ （舍去）
因为 $\text{[math]}$ ，此时， $\text{[math]}$ ，
所以 $\text{[math]}$ ，故取 m= $\text{[math]}$ ，
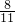当x=3时，f（x）_min=1，即 $\text{[math]}$ ．故取n=3
综上，取m= 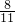$\text{[math]}$ ，n=3时，f（x）=-2x²+7x-2在[ 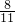$\text{[math]}$ ，3]上的值域是[1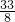， $\text{[math]}$ ]．…（14分）
分析：（1）根据二次函数f（x）=ax²+bx+a满足条件 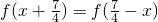$\text{[math]}$ ，可知函数的对称轴，利用方程f（x）=7x+a有两个相等的实根，可得其判别式为0，从而可求f（x）的解析式；
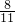（2）构建函数 $\text{[math]}$ （x＞0），则当f（x）=g（x）时，即 $\text{[math]}$ ，利用 $\text{[math]}$ ，此时， $\text{[math]}$ ，可知 $\text{[math]}$ ，故取 m= $\text{[math]}$ ，当x=3时，f（x）_min=1，即 $\text{[math]}$ ．故取n=3，从而问题得解．
点评：本题重点考查函数的解析式，考查函数的定义域与值域，考查存在性问题，考查数形结合的思想，综合性强．