题目内容
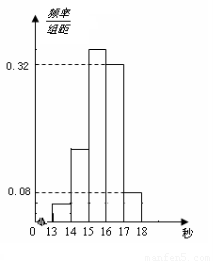
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18]。按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8。
(Ⅰ)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(Ⅱ)求调查中随机抽取了多少个学生的百米成绩;
(Ⅲ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率。
(Ⅰ)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(Ⅱ)求调查中随机抽取了多少个学生的百米成绩;
(Ⅲ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率。

解:(Ⅰ)百米成绩在[16,17)内的频率为0.321=0.32
0.32×1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人;
(Ⅱ)设图中从左到右前3个组的频率分别为3x,8x ,19x 依题意,得
3x+8x+19x+0.321+0.081=1 ,∴x=0.02
设调查中随机抽取了n 个学生的百米成绩,则8×0.02= ∴n=50
∴n=50
∴调查中随机抽取了50个学生的百米成绩
(Ⅲ)百米成绩在第一组的学生数有3×0.02×1×50=3,记他们的成绩为a,b,c
百米成绩在第五组的学生数有0.08×1×50= 4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q}, {m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21个
其中满足成绩的差的绝对值大于1秒所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个, 所以P= =
=
0.32×1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人;
(Ⅱ)设图中从左到右前3个组的频率分别为3x,8x ,19x 依题意,得
3x+8x+19x+0.321+0.081=1 ,∴x=0.02
设调查中随机抽取了n 个学生的百米成绩,则8×0.02=
 ∴n=50
∴n=50 ∴调查中随机抽取了50个学生的百米成绩
(Ⅲ)百米成绩在第一组的学生数有3×0.02×1×50=3,记他们的成绩为a,b,c
百米成绩在第五组的学生数有0.08×1×50= 4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q}, {m,n},{m,p},{m,q},{n,p},{n,q},{p,q},共21个
其中满足成绩的差的绝对值大于1秒所包含的基本事件有{a,m},{a,n},{a,p},{a,q},{b,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个, 所以P=
 =
=

练习册系列答案
相关题目
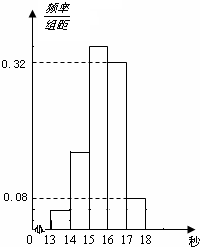 为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.