题目内容

已知f（x）=ax2+bx+1．
（1）若f（x）＞0的解集是（-1，2），求实数a，b的值．
（2）若A={x|f（x）＞0}，且-1∈A，2∈A，求3a-b的取值范围．

精英家教网
（1）由题意可知：a＜0，且ax2+bx+1=0的解为-1，2
∴
a＜0
1
a
=-2
-
b
a
=1
解得：a=-
1
2
，b=
1
2

（2）由题意可得
f(-1)＞0
f(2)＞0
，?
a-b+1＞0
4a+2b+1＞0

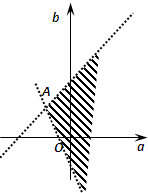
画出可行域，由
a-b+1=0
4a+2b+1=0

得{
a=-
1
2
b=
1
2

作平行直线系z=3a-b可知z=3a-b的取值范围是（-2，+∞）
练习册系列答案
相关题目
例2：已知f（x）=ax2+bx+c的图象过点（-1，0），是否存在常数a、b、c，使不等式x≤f（x）≤
x2+12
对一切实数x都成立？
已知f（x）=ax2+bx，若1≤f（1）≤3，-1≤f（-1）≤1，则f（2）的取值范围是
[2，10]
[2，10]
．
已知f（x）=ax2-blnx+2x（a＞0，b＞0）在区间(
1
2
，1)上不单调，则
3b-2
3a+2
的取值范围是（　　）
已知f（x）=ax2+bx+c（a≠0），g（x）=f[f（x）]
①若f（x）无零点，则g（x）＞0对?x∈R成立；
②若f（x）有且只有一个零点，则g（x）必有两个零点；
③若方程f（x）=0有两个不等实根，则方程g（x）=0不可能无解
其中真命题的个数是（　　）
已知f（x）=ax2-3ax+a2-1（a＜0），则f（3），f（-3），f（
3
2
）从小到大的顺序是
f（-3）＜f（3）＜f（
3
2
）
f（-3）＜f（3）＜f（
3
2
）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网