Question

【题目】三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为；直线SB与AC所成角的余弦值为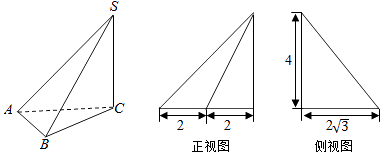

Answer 1

【答案】4 ；
【解析】解：由已知中的三视图可得SC⊥平面ABC， 且底面△ABC为等腰三角形，
在△ABC中AC=4，AC边上的高为2 ，
故BC=4，∠ACB=60°
在Rt△SBC中，由SC=4，可得SB=4 ，
建立如图所示的坐标系，则S（0，0，4），B（2 ，﹣2，0），A（0，﹣4，0），C（0，0，0），
∴ =（2 ，﹣2，﹣4）， =（0，4，0），
∴直线SB与AC所成角的余弦值为| |= ．
所以答案是4 ， ．

【考点精析】关于本题考查的简单空间图形的三视图，需要了解画三视图的原则：长对齐、高对齐、宽相等才能得出正确答案．