题目内容
已知函数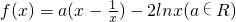 .
.
(1)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调区间;
(3)设函数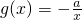 .若至少存在一个x0∈[1,e],使得f(x0)>g(x0)成立,求实数a的取值范围.
.若至少存在一个x0∈[1,e],使得f(x0)>g(x0)成立,求实数a的取值范围.
解:函数的定义域为(0,+∞),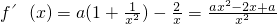 .
.
(1)当a=2时,函数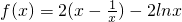 ,f′(x)=
,f′(x)= ,
,
因为f(1)=0,f'(1)=2.
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-0=2(x-1),即2x-y-2=0.
(2)函数f(x)的定义域为(0,+∞).
①当a≤0时,h(x)=ax2-2x+a<0在(0,+∞)上恒成立,
则f'(x)<0在(0,+∞)上恒成立,
此时f(x)在(0,+∞)上单调递减.
②当a>0时,△=4-4a2,
(ⅰ)若0<a<1,
由f'(x)>0,即h(x)>0,得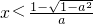 或
或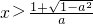 ;
;
由f'(x)<0,即h(x)<0,得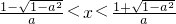 .
.
所以函数f(x)的单调递增区间为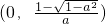 和
和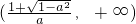 ,
,
单调递减区间为 .
.
(ⅱ)若a≥1,h(x)≥0在(0,+∞)上恒成立,则f'(x)≥0在(0,+∞)上恒成立,此时f(x)在(0,+∞)上单调递增.
(3))因为存在一个x0∈[1,e]使得f(x0)>g(x0),
则ax0>2lnx0,等价于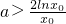 .
.
令 ,等价于“当x∈[1,e]时,a>F(x)min”.
,等价于“当x∈[1,e]时,a>F(x)min”.
对F(x)求导,得 .
.
因为当x∈[1,e]时,F'(x)≥0,所以F(x)在[1,e]上单调递增.
所以F(x)min=F(1)=0,因此a>0.
分析:(1)当a=2时求出f(1),切线斜率k=f′(1),利用点斜式即可求得切线方程;
(2)求出函数定义域,分①当a≤0,②当a>0两种情况讨论解不等式f'(x)>0,f'(x)<0即可;
(3)存在一个x0∈[1,e]使得f(x0)>g(x0),则ax0>2lnx0,等价于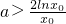 ,令
,令 ,等价于“当x∈[1,e]时,a>F(x)min”.利用导数易求其最小值.
,等价于“当x∈[1,e]时,a>F(x)min”.利用导数易求其最小值.
点评:本题考查导数的几何意义、导数研究函数单调性及求函数的最值问题,考查学生分析问题解决问题的能力,对于“能成立”问题及“恒成立”问题往往转化为函数最值解决.
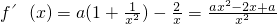 .
. (1)当a=2时,函数
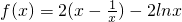 ,f′(x)=
,f′(x)= ,
,因为f(1)=0,f'(1)=2.
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-0=2(x-1),即2x-y-2=0.
(2)函数f(x)的定义域为(0,+∞).
①当a≤0时,h(x)=ax2-2x+a<0在(0,+∞)上恒成立,
则f'(x)<0在(0,+∞)上恒成立,
此时f(x)在(0,+∞)上单调递减.
②当a>0时,△=4-4a2,
(ⅰ)若0<a<1,
由f'(x)>0,即h(x)>0,得
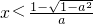 或
或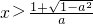 ;
; 由f'(x)<0,即h(x)<0,得
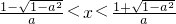 .
.所以函数f(x)的单调递增区间为
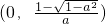 和
和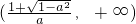 ,
,单调递减区间为
 .
. (ⅱ)若a≥1,h(x)≥0在(0,+∞)上恒成立,则f'(x)≥0在(0,+∞)上恒成立,此时f(x)在(0,+∞)上单调递增.
(3))因为存在一个x0∈[1,e]使得f(x0)>g(x0),
则ax0>2lnx0,等价于
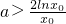 .
.令
 ,等价于“当x∈[1,e]时,a>F(x)min”.
,等价于“当x∈[1,e]时,a>F(x)min”.对F(x)求导,得
 .
.因为当x∈[1,e]时,F'(x)≥0,所以F(x)在[1,e]上单调递增.
所以F(x)min=F(1)=0,因此a>0.
分析:(1)当a=2时求出f(1),切线斜率k=f′(1),利用点斜式即可求得切线方程;
(2)求出函数定义域,分①当a≤0,②当a>0两种情况讨论解不等式f'(x)>0,f'(x)<0即可;
(3)存在一个x0∈[1,e]使得f(x0)>g(x0),则ax0>2lnx0,等价于
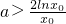 ,令
,令 ,等价于“当x∈[1,e]时,a>F(x)min”.利用导数易求其最小值.
,等价于“当x∈[1,e]时,a>F(x)min”.利用导数易求其最小值.点评:本题考查导数的几何意义、导数研究函数单调性及求函数的最值问题,考查学生分析问题解决问题的能力,对于“能成立”问题及“恒成立”问题往往转化为函数最值解决.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
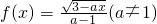 .
.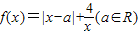 .
.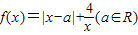 .
.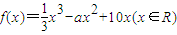 .
.