题目内容
已知向量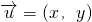 与向量
与向量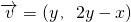 的对应关系可用
的对应关系可用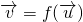 表示.
表示.
(1)设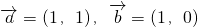 ,求向量
,求向量 的坐标;
的坐标;
(2)证明:对于任意向量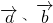 及常数m、n,恒有
及常数m、n,恒有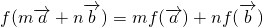 成立;
成立;
(3)求使 成立的向量
成立的向量 .
.
解:(1)f( )=(1,2-1)=(1,1),f(
)=(1,2-1)=(1,1),f( )=(0,2×0-1)=(0,-1),
)=(0,2×0-1)=(0,-1),
∴ .
.
(2)设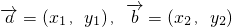 ,∴m
,∴m +n
+n =(mx1+nx2,my1+ny2 ),
=(mx1+nx2,my1+ny2 ),
∴f(m +n
+n )=( my1+ny2,2my1+2ny2-mx1-nx2 ),
)=( my1+ny2,2my1+2ny2-mx1-nx2 ),
∴mf( )+nf(
)+nf( )=m(y1,2y1-x1 )+n(y2,2y2-x2 )=( my1+ny2,2my1+2ny2-mx1-nx2 ),
)=m(y1,2y1-x1 )+n(y2,2y2-x2 )=( my1+ny2,2my1+2ny2-mx1-nx2 ),
∴对于任意向量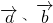 及常数m、n,
及常数m、n,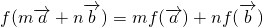 成立.
成立.
(3)设 =(x,y),则 f(
=(x,y),则 f( )=(y,2y-x),∴
)=(y,2y-x),∴ ,
,
∴x=1,y=3,∴ .
.
分析:(1)直接利用题中的对应关系求出 f( )=(1,2-1)=(1,1),f(
)=(1,2-1)=(1,1),f( )=(0,2×0-1)=(0,-1),
)=(0,2×0-1)=(0,-1),
(2) 设出任意向量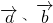 的坐标,分别计算要证等式的左边的右边,比较计算结果可得等式成立.
的坐标,分别计算要证等式的左边的右边,比较计算结果可得等式成立.
(3)设 =(x,y),则 f(
=(x,y),则 f( )=(y,2y-x),∴
)=(y,2y-x),∴ ,解方程可求向量
,解方程可求向量 的坐标.
的坐标.
点评:本题考查两个向量坐标形式的运算,以及用待定系数法求向量的坐标.
 )=(1,2-1)=(1,1),f(
)=(1,2-1)=(1,1),f( )=(0,2×0-1)=(0,-1),
)=(0,2×0-1)=(0,-1),∴
 .
.(2)设
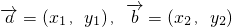 ,∴m
,∴m +n
+n =(mx1+nx2,my1+ny2 ),
=(mx1+nx2,my1+ny2 ),∴f(m
 +n
+n )=( my1+ny2,2my1+2ny2-mx1-nx2 ),
)=( my1+ny2,2my1+2ny2-mx1-nx2 ),∴mf(
 )+nf(
)+nf( )=m(y1,2y1-x1 )+n(y2,2y2-x2 )=( my1+ny2,2my1+2ny2-mx1-nx2 ),
)=m(y1,2y1-x1 )+n(y2,2y2-x2 )=( my1+ny2,2my1+2ny2-mx1-nx2 ),∴对于任意向量
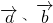 及常数m、n,
及常数m、n,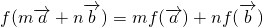 成立.
成立.(3)设
 =(x,y),则 f(
=(x,y),则 f( )=(y,2y-x),∴
)=(y,2y-x),∴ ,
,∴x=1,y=3,∴
 .
.分析:(1)直接利用题中的对应关系求出 f(
 )=(1,2-1)=(1,1),f(
)=(1,2-1)=(1,1),f( )=(0,2×0-1)=(0,-1),
)=(0,2×0-1)=(0,-1),(2) 设出任意向量
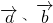 的坐标,分别计算要证等式的左边的右边,比较计算结果可得等式成立.
的坐标,分别计算要证等式的左边的右边,比较计算结果可得等式成立.(3)设
 =(x,y),则 f(
=(x,y),则 f( )=(y,2y-x),∴
)=(y,2y-x),∴ ,解方程可求向量
,解方程可求向量 的坐标.
的坐标.点评:本题考查两个向量坐标形式的运算,以及用待定系数法求向量的坐标.

练习册系列答案
相关题目

 与向量
与向量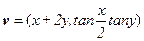 的对应关系可用
的对应关系可用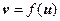 表示.试问是否存在向量
表示.试问是否存在向量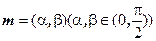 ,使得
,使得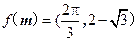 成立?如果存在,求出向量
成立?如果存在,求出向量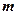 ;如果不存在,请说明理由.
;如果不存在,请说明理由.
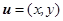 与向量
与向量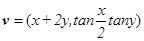 的对应关系可用
的对应关系可用 表示.试问是否存在向量
表示.试问是否存在向量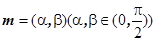 ,使得
,使得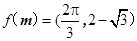 成立?如果存在,求出向量
成立?如果存在,求出向量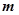 ;如果不存在,请说明理由.
;如果不存在,请说明理由. 与向量
与向量 的对应关系可用
的对应关系可用 表示.
表示. ,求向量
,求向量 的坐标;
的坐标; 及常数m、n,恒有
及常数m、n,恒有 成立;
成立; 成立的向量
成立的向量 .
.