题目内容
集合A是由具备下列性质的函数f(x)组成的:
①函数f(x)的定义域是[0,+∞);
②函数f(x)的值域是[﹣2,4);
③函数f(x)在[0,+∞)上是增函数,试分别探究下列两小题:
(1)判断函数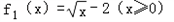 及
及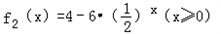 是否属于集合A?并简要说明理由;
是否属于集合A?并简要说明理由;
(2)对于(1)中你认为属于集合A的函数f(x),不等式f(x)+f(x+2)<2f(x+1)是否对于任意的x≥0恒成立?若成立,请给出证明;若不成立,请说明理由.
①函数f(x)的定义域是[0,+∞);
②函数f(x)的值域是[﹣2,4);
③函数f(x)在[0,+∞)上是增函数,试分别探究下列两小题:
(1)判断函数
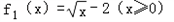 及
及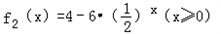 是否属于集合A?并简要说明理由;
是否属于集合A?并简要说明理由;(2)对于(1)中你认为属于集合A的函数f(x),不等式f(x)+f(x+2)<2f(x+1)是否对于任意的x≥0恒成立?若成立,请给出证明;若不成立,请说明理由.
解:(1)∵函数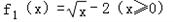 的值域[﹣2,+∞)
的值域[﹣2,+∞)
∴f1(x)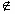 A
A
对于f2(x),定义域为[0,+∞),满足条件①.
而由x≥0知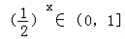 ,
,
∴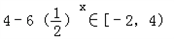 ,满足条件②
,满足条件②
又∵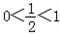 ,
,
∴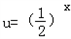 在[0,+∞)上是减函数
在[0,+∞)上是减函数
.∴f2(x)在[0,+∞)上是增函数,满足条件③
∴f2(x)属于集合A.
(2)f2(x)属于集合A,
原不等式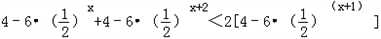 对任意x≥0总成立
对任意x≥0总成立
证明:由(1)知,f2(x)属于集合A.
∴原不等式为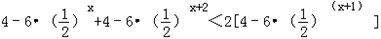
整理为: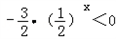 .
.
∵对任意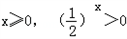 ,
,
∴原不等式对任意x≥0总成立

练习册系列答案
相关题目
 -2(x≥0)及f2(x)=4-6·
-2(x≥0)及f2(x)=4-6· x(x≥0)是否属于集合A?并简要说明理由;
x(x≥0)是否属于集合A?并简要说明理由;