题目内容
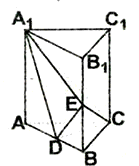 如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E为BB1中点,∠A1DE=90°.
如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E为BB1中点,∠A1DE=90°.
(I)求证:CD⊥平面A1ABB1;
(II)求二面角C-A1E-D的大小.
(I)证明:连接AE.在△ABC中,用勾股定理,求出AB=2
在△A1B1E中,用勾股定理,求出AE=3.
在△AA1D中,有:A1D2=AA12+AD2
在△BDE中,有:DE2=BE2+BD2
在△A1DE中,有AE2=A1D2+DE2=(AA12+AD2)+(BE2+BD2)
AB=AD+BD(与上式联立,解方程组)
可以求出:AD=BD= .即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,
.即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,
也就是斜边上的高(CD⊥AB).
又在直三菱柱ABC-A1B1C1中,有AA1⊥底面ABC,又CD∈面ABC,则AA1⊥CD.
综合上述条件,CD⊥AB,CD⊥AA1,且AA1∩AB=A.,有CD⊥面A1ABB1
(II)过D作DH⊥A1E于H,AC=BC=AA1=2,A1E=3,DE= ,A1D=
,A1D= ,DH=
,DH=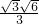 =
=
所以,二面角C-A1E-D的正切值为: =1,二面角C-A1E-D的大小为45°
=1,二面角C-A1E-D的大小为45°
分析:(I)证明:连接AE.求出AB=2 求出AE=3.求出:AD=BD=
求出AE=3.求出:AD=BD= .即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,
.即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,
证明CD⊥AB,CD⊥AA1,且AA1∩AB=A,即可得到CD⊥面A1ABB.
(II)过D作DH⊥A1E于H,求出A1E=3,DE,A1D,DH,即可求出二面角C-A1E-D的正切值为: =1,二面角C-A1E-D的大小为45°
=1,二面角C-A1E-D的大小为45°
点评:本小题主要考查空间线面关系、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

在△A1B1E中,用勾股定理,求出AE=3.
在△AA1D中,有:A1D2=AA12+AD2

在△BDE中,有:DE2=BE2+BD2
在△A1DE中,有AE2=A1D2+DE2=(AA12+AD2)+(BE2+BD2)
AB=AD+BD(与上式联立,解方程组)
可以求出:AD=BD=
 .即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,
.即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,也就是斜边上的高(CD⊥AB).
又在直三菱柱ABC-A1B1C1中,有AA1⊥底面ABC,又CD∈面ABC,则AA1⊥CD.
综合上述条件,CD⊥AB,CD⊥AA1,且AA1∩AB=A.,有CD⊥面A1ABB1
(II)过D作DH⊥A1E于H,AC=BC=AA1=2,A1E=3,DE=
 ,A1D=
,A1D= ,DH=
,DH=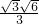 =
=
所以,二面角C-A1E-D的正切值为:
 =1,二面角C-A1E-D的大小为45°
=1,二面角C-A1E-D的大小为45°分析:(I)证明:连接AE.求出AB=2
 求出AE=3.求出:AD=BD=
求出AE=3.求出:AD=BD= .即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,
.即D点是AB的中点,CD是等腰RT△ABC的斜边AB上的中线,证明CD⊥AB,CD⊥AA1,且AA1∩AB=A,即可得到CD⊥面A1ABB.
(II)过D作DH⊥A1E于H,求出A1E=3,DE,A1D,DH,即可求出二面角C-A1E-D的正切值为:
 =1,二面角C-A1E-D的大小为45°
=1,二面角C-A1E-D的大小为45°点评:本小题主要考查空间线面关系、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.