题目内容
设地球的半径为R，赤道上东经40°的点A与北纬45°、东经130°的点B的球面距离是分析：画出图形，通过三面角公式求出∠AOB，即可求出A、B两点的球面距离．
解答：
解：如图，C是赤道面内，B在上的射影，
由题意∠BOC=90°，∠AOC=45°，
所以有三面角公式可得：cos∠AOB=cos90°cos45°=0，
所以∠AOB=
；
A、B两点的球面距离是：R（
）．
故答案为：
R．
解：如图，C是赤道面内，B在上的射影，由题意∠BOC=90°，∠AOC=45°，
所以有三面角公式可得：cos∠AOB=cos90°cos45°=0，
所以∠AOB=
| π |
| 2 |
A、B两点的球面距离是：R（
| π |
| 2 |
故答案为：
| π |
| 2 |
点评：本题是基础题，考查球面距离的求法，考查空间想象能力，计算能力．
练习册系列答案
相关题目
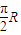，若A地为东经0°，则B地的经度为 ．