题目内容
在区间 内随机取两个数分别记为
内随机取两个数分别记为 ,则使得函数
,则使得函数
有零点的概率为 ( )
A. | B. | C. | D. |
B
解析试题分析:由题意知本题是一个几何概型,∵ 使得函数
使得函数 有零点,∴
有零点,∴ ∴
∴ ,试验发生时包含的所有事件是
,试验发生时包含的所有事件是 ∴
∴ ,而满足条件的事件是
,而满足条件的事件是 ,∴
,∴ , 由几何概型公式得到
, 由几何概型公式得到 ,故选
,故选 .
.
考点:1.函数零点问题;2.几何概型.

练习册系列答案
相关题目
下列四个判断:
①某校高三(1)班的人和高三(2)班的人数分别是 ,某次测试数学平均分分别是
,某次测试数学平均分分别是 ,则这两个班的数学平均分为
,则这两个班的数学平均分为 ;
;
②从总体中抽取的样本 则回归直线
则回归直线 必过点
必过点 ;
;
③已知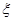 服从正态分布
服从正态分布 ,且
,且 ,则
,则
其中正确的个数有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
函数 ,定义域内任取一点
,定义域内任取一点 ,使
,使 的概率是( )
的概率是( )
A. | B. | C. | D. |
已知某一随机变量X的概率分布如下,且E(X)=6.9,则a的值为 ( )
| X | 4 | a | 9 |
| P | m | 0.2 | 0.5 |












 的分布列为
的分布列为


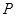



 ( )
( ) B.
B. D.
D.