题目内容
以椭圆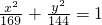
的右焦点为圆心，且与双曲线
的渐近线相切的圆的方程为________．
（x-5）2+y2=16
分析：求出椭圆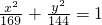的右焦点得到圆心，再求出双曲线的渐近线，由圆心到渐近线的距离得到圆的半径，由此可以得到圆的方程．
解答：∵c2=169-144=25，∴椭圆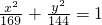的右焦点为F（5，0），
∴所求圆的圆心坐标是（5，0）．
∵双曲线的渐近线方程是
，
由点到直线的距离公式可知（5，0）到的距离
=4，
∴所求圆的半径为4．
故所求圆的方程是（x-5）2+y2=16．
答案：（x-5）2+y2=16．
点评：求出圆的圆心和半径，就得到圆的方程．
分析：求出椭圆
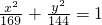的右焦点得到圆心，再求出双曲线的渐近线，由圆心到渐近线的距离得到圆的半径，由此可以得到圆的方程．解答：∵c2=169-144=25，∴椭圆
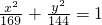的右焦点为F（5，0），∴所求圆的圆心坐标是（5，0）．
∵双曲线
的渐近线方程是，由点到直线的距离公式可知（5，0）到
的距离=4，∴所求圆的半径为4．
故所求圆的方程是（x-5）2+y2=16．
答案：（x-5）2+y2=16．
点评：求出圆的圆心和半径，就得到圆的方程．
练习册系列答案
相关题目
的椭圆
上有一点
到椭圆两焦点的距离和为
.以椭圆
的右焦点
为圆心，短轴长为直径的圆有切线
（
为切点），且点
满足
（
为椭圆
.
为圆心作一个圆，使此圆过椭圆中心并交椭圆于点M，N，
的直线MF1是圆
的右焦点为圆心，且与双曲线
的渐近线相切的圆的方程是（ ）
B.
D.
为圆心作一个圆过椭圆
的直线
是圆的切线，则椭圆的右
与圆
的右焦点为圆心，且与双曲线
的渐近线相切的圆的方程是 （ ）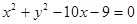
B．
D．