题目内容
已知椭圆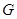 :
: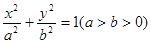 的离心率为
的离心率为 ,过椭圆
,过椭圆 右焦点
右焦点 的直线
的直线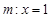 与椭圆
与椭圆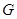 交于点
交于点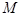 (点
(点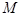 在第一象限).
在第一象限).
(Ⅰ)求椭圆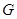 的方程;
的方程;
(Ⅱ)已知 为椭圆
为椭圆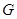 的左顶点,平行于
的左顶点,平行于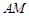 的直线
的直线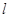 与椭圆相交于
与椭圆相交于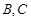 两点.判断直线
两点.判断直线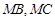 是否关于直线
是否关于直线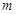 对称,并说明理由.
对称,并说明理由.
(Ⅰ)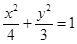 (Ⅱ)对称
(Ⅱ)对称
解析试题分析:(Ⅰ)由圆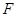 方程可知圆心为
方程可知圆心为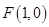 ,即
,即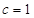 ,又因为离心率为
,又因为离心率为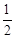 ,可得
,可得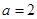 ,根据椭圆中关系式
,根据椭圆中关系式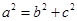 ,可求
,可求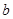 。椭圆方程即可求出。因为
。椭圆方程即可求出。因为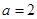 ,则右顶点为
,则右顶点为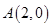 ,将其代入圆的方程可求半径
,将其代入圆的方程可求半径 。(Ⅱ)由椭圆方程可知
。(Ⅱ)由椭圆方程可知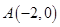 ,将
,将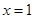 代入椭圆方程可得
代入椭圆方程可得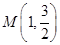 。可得
。可得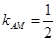 ,设直线
,设直线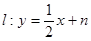 ,然后和椭圆方程联立,消掉y(或x)得到关于x的一元二次方程。再根据韦达定理得出根与系数的关系。可得两直线
,然后和椭圆方程联立,消掉y(或x)得到关于x的一元二次方程。再根据韦达定理得出根与系数的关系。可得两直线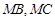 的斜率。当直线
的斜率。当直线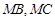 是否关于直线
是否关于直线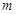 对称时两直线倾斜角互补,所以斜率互为相反数。把求得的两直线斜率相加若为0,则说明两直线对称。否则不对称。
对称时两直线倾斜角互补,所以斜率互为相反数。把求得的两直线斜率相加若为0,则说明两直线对称。否则不对称。
试题解析:(Ⅰ)由题意得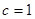 , 1分
, 1分
由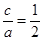 可得
可得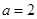 , 2分
, 2分
所以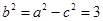 , 3分
, 3分
所以椭圆的方程为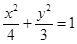 . 4分
. 4分
(Ⅱ)由题意可得点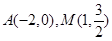 , 6分
, 6分
所以由题意可设直线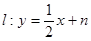 ,
,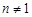 . 7分
. 7分
设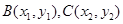 ,
,
由 得
得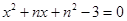 .
.
由题意可得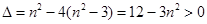 ,即
,即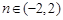 且
且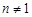 . 8分
. 8分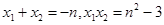 . 9分
. 9分
因为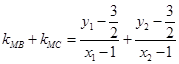 10分
10分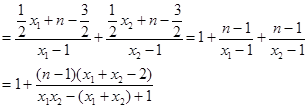
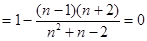 , 13分
, 13分
所以直线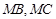 关于直线
关于直线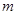 对称. 14分
对称. 14分
考点:椭圆的基础知识、直线与椭圆的位置关系,考查分析问题、解决问题以及化归与转化的能力,考查综合素质。

练习册系列答案
相关题目
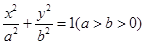 的左、右焦点分别为
的左、右焦点分别为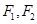 ,离心率为
,离心率为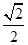 ,P是椭圆上一点,且
,P是椭圆上一点,且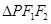 面积的最大值等于2.
面积的最大值等于2.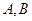 是抛物线
是抛物线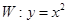 上的两个点,点
上的两个点,点 的坐标为
的坐标为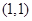 ,直线
,直线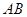 的斜率为k,
的斜率为k,  为坐标原点.
为坐标原点.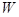 的焦点在直线
的焦点在直线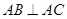 ,过
,过 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为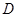 ,求
,求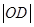 的最小值.
的最小值.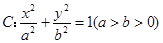 经过点
经过点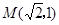 ,离心率为
,离心率为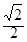 .
.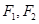 是椭圆E:
是椭圆E: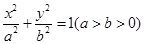 的两个焦点,抛物线
的两个焦点,抛物线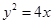 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y=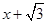 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,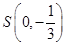 的动直线
的动直线 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。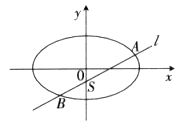
 的离心率与等轴双曲线的离心率互为倒数,直线
的离心率与等轴双曲线的离心率互为倒数,直线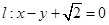 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。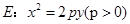 ,直线
,直线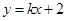 与E交于A、B两点,且
与E交于A、B两点,且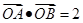 ,其中O为原点.
,其中O为原点.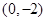 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为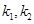 ,证明:
,证明: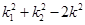 为定值.
为定值.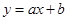 与双曲线
与双曲线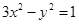 交于A、B,且以AB为直径的圆过原点,求点
交于A、B,且以AB为直径的圆过原点,求点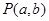 的轨迹方程.
的轨迹方程.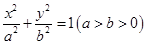 的左右两焦点分别为
的左右两焦点分别为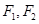 ,
,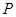 是椭圆上一点,且在
是椭圆上一点,且在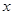 轴上方,
轴上方,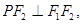
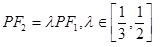 .
.
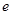 的取值范围;
的取值范围;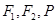 的圆
的圆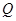 的截
的截 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;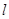 上任一点
上任一点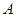 引圆
引圆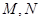 .试探究直线
.试探究直线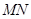 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由.