题目内容
已知函数f(x)=lnx.(1)若函数F(x)=mf(x)+3x-2x2在x=1处取得极值,求函数F(x)的单调区间;
(2)设函数G(x)=f(x)+
 ,若对任意x∈(0,1),都有G(x)<0成立,求实数a的取值范围.
,若对任意x∈(0,1),都有G(x)<0成立,求实数a的取值范围.
【答案】分析:(1)因为函数一个极值点已知,令f′(x)=0,把x=1代入求出m,再利用函数的导数确定函数的单调区间,f′(x)大于零和小于零分别求出递增和递减区间即可;
(2)先把问题转化为m(x)=x2+(2-4a)x+1<0对x∈(0,1)恒成立,再把m(x)=x2+(2-4a)x+1看成x的二次函数,找到m(x)<0恒成立的条件,解之即可求实数a的取值范围.
解答:解:(1)函数F(x)=mlnx+3x-2x2,其定义域为(0,+∞)
F'(x)=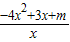 由 F'(1)=0 得:m=1 …(2分)
由 F'(1)=0 得:m=1 …(2分)
∴F'(x)=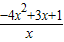 =
=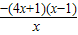
当x∈(0,1),F'(x)>0,函数F(x)单调递增,
当x∈(1,+∞),F'(x)<0,函数F(x)单调递减,
∴函数F(x)的单调递增区间为(0,1);函数F(x)的单调递减区间为(1,+∞)…(6分)
(2)∵G'(x)=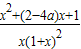 …(7分)
…(7分)
设m(x)=x2+(2-4a)x+1,方程m(x)=0的判别式△=16a(a-1).
若a∈(0,1],△≤0,m(x)≥0,G'(x)≥0,G'(x)在(0,1)上是增函数,
又G(1)=0,所以x∈(0,1),G(x)<0.…(9分)
若a∈(1,+∞),∵△>0,m(0)=1>0,m(1)=4(1-a)<0,
∴g(x)在(0,1)上不是单调函数.
所以存在x∈(0,1),使得m(x)=0,对任意x∈(x,1),m(x)<0,
即G'(x)<0,G(x)在(x,1)上是减函数,
又G(1)=0,所以x∈(x,1),G(x)<0.不合题意.
综上,实数a的取值范围是(0,1]…(12分)
点评:考查函数在某点取得极值的条件、利用导数研究函数的单调性、利用导数研究函数的极值,属于中档题.
(2)先把问题转化为m(x)=x2+(2-4a)x+1<0对x∈(0,1)恒成立,再把m(x)=x2+(2-4a)x+1看成x的二次函数,找到m(x)<0恒成立的条件,解之即可求实数a的取值范围.
解答:解:(1)函数F(x)=mlnx+3x-2x2,其定义域为(0,+∞)
F'(x)=
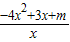 由 F'(1)=0 得:m=1 …(2分)
由 F'(1)=0 得:m=1 …(2分)∴F'(x)=
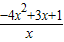 =
=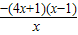
当x∈(0,1),F'(x)>0,函数F(x)单调递增,
当x∈(1,+∞),F'(x)<0,函数F(x)单调递减,
∴函数F(x)的单调递增区间为(0,1);函数F(x)的单调递减区间为(1,+∞)…(6分)
(2)∵G'(x)=
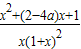 …(7分)
…(7分)设m(x)=x2+(2-4a)x+1,方程m(x)=0的判别式△=16a(a-1).
若a∈(0,1],△≤0,m(x)≥0,G'(x)≥0,G'(x)在(0,1)上是增函数,
又G(1)=0,所以x∈(0,1),G(x)<0.…(9分)
若a∈(1,+∞),∵△>0,m(0)=1>0,m(1)=4(1-a)<0,
∴g(x)在(0,1)上不是单调函数.
所以存在x∈(0,1),使得m(x)=0,对任意x∈(x,1),m(x)<0,
即G'(x)<0,G(x)在(x,1)上是减函数,
又G(1)=0,所以x∈(x,1),G(x)<0.不合题意.
综上,实数a的取值范围是(0,1]…(12分)
点评:考查函数在某点取得极值的条件、利用导数研究函数的单调性、利用导数研究函数的极值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目