题目内容
命题(1)x+ 的最小值是2;(2)
的最小值是2;(2) 的最小值是2;(3)
的最小值是2;(3) 的最小值是2;(4)2-3x-
的最小值是2;(4)2-3x- 的最小值是2;其中正确的有( )个.
的最小值是2;其中正确的有( )个.A.1
B.2
C.3
D.4
【答案】分析:对于选项(1)中的x来说,因为x不等于0,所以x大于0小于0不确定,所以最小值不一定为2;对于选项(2) =
= 利用基本不等式可能性求得其最小值;对于选项(3)中的函数来说,
利用基本不等式可能性求得其最小值;对于选项(3)中的函数来说, 也大于0,但是基本不等式不满足取等号的条件;选项D中的x来说,因为x不等于0,所以x大于0小于0不确定,所以最小值不一定为2;.
也大于0,但是基本不等式不满足取等号的条件;选项D中的x来说,因为x不等于0,所以x大于0小于0不确定,所以最小值不一定为2;.
解答:解:对于A:不能保证x>0,故错;
对于B: =
= ≥2,当x=0时等号成立,故
≥2,当x=0时等号成立,故 的最小值是2,
的最小值是2,
对于C:y= +
+
 ,当x2+4=1时等号成立,矛盾,即最小值大于2,故C不正确;
,当x2+4=1时等号成立,矛盾,即最小值大于2,故C不正确;
对于D:不能保证x>0,故错.
故选A.
点评:本题考查命题的真假的判定,考查分析问题解决问题的能力,解决此类问题往往是逐一进行判定.本题主要考查基本不等式的应用.应用基本不等式时一定要验证“一正、二定、三相等”,这是基本不等式的基本条件.
 =
= 利用基本不等式可能性求得其最小值;对于选项(3)中的函数来说,
利用基本不等式可能性求得其最小值;对于选项(3)中的函数来说, 也大于0,但是基本不等式不满足取等号的条件;选项D中的x来说,因为x不等于0,所以x大于0小于0不确定,所以最小值不一定为2;.
也大于0,但是基本不等式不满足取等号的条件;选项D中的x来说,因为x不等于0,所以x大于0小于0不确定,所以最小值不一定为2;.解答:解:对于A:不能保证x>0,故错;
对于B:
 =
= ≥2,当x=0时等号成立,故
≥2,当x=0时等号成立,故 的最小值是2,
的最小值是2,对于C:y=
 +
+
 ,当x2+4=1时等号成立,矛盾,即最小值大于2,故C不正确;
,当x2+4=1时等号成立,矛盾,即最小值大于2,故C不正确;对于D:不能保证x>0,故错.
故选A.
点评:本题考查命题的真假的判定,考查分析问题解决问题的能力,解决此类问题往往是逐一进行判定.本题主要考查基本不等式的应用.应用基本不等式时一定要验证“一正、二定、三相等”,这是基本不等式的基本条件.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 ,(a是常数且a>0).于下列命题:
,(a是常数且a>0).于下列命题: 的最小值是2;(2)
的最小值是2;(2)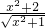 的最小值是2;(3)
的最小值是2;(3) 的最小值是2;(4)2-3x-
的最小值是2;(4)2-3x- 的最小值是2;其中正确的有____个.
的最小值是2;其中正确的有____个.