Question

（本题满分14分）已知函数(m≥1)

（1）若曲线C: 在点 P处的切线与C有且只有一个公共点，求m的值。

（2）求证：存在单调递减区间，并求出单调递减区间的长度的取值范围。

Answer 1

(本题满分14分)

解解：（1）的定义域为

       

       

        在点P处的切线的方程为：  

        由题意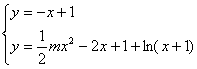有且只有一个实根

        即：有且只有一个实数根  …..2分

        显然是方程的一个根

        令

       

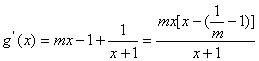
当时，（仅时取“=”）

在单调递增

是方程的唯一一个实数根                       （4分）

当时，令，得，

当x变化时，的变化情况如下表：

				0
	+	0	-	0	+
				0

又当时，

在及处均有一个根，不合题意 ………6分

综上，m=1.                                         …………7分

    (2) =

    令            _9分

   

    又的对称轴且

    在内有两个不同实根

    即的解集为   

    有单调递减区间                     _{………11分}

   

                                   _{………….13分}

   

的递减区间的长度范围为      _{…… 14分.}