题目内容
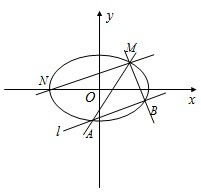
已知椭圆C经过点M ,其左顶点为N,两个焦点为(-1,0),(1,0),平行于MN的直线l交椭圆于A,B两个不同的点.
,其左顶点为N,两个焦点为(-1,0),(1,0),平行于MN的直线l交椭圆于A,B两个不同的点.(Ⅰ)求椭圆C的方程;
(Ⅱ)求证:直线MA,MB与x轴始终围成一个等腰三角形.

【答案】分析:(Ⅰ)由题意设出椭圆方程,把点M的坐标代入椭圆方程,结合隐含条件a2=b2+c2可求解a2,b2,则椭圆的方程可求;
(Ⅱ)由椭圆方程求出顶点N的坐标,求出MN的斜率,设出直线l的斜截式方程,和椭圆联立后利用根与系数的关系求出A,B两点的横坐标的和与积,由两点式写出MA和MB的斜率,作和后化为含有直线l的截距的代数式,整理得到结果为0,所以结论得证.
解答:(Ⅰ)解:设椭圆的方程为 (a>b>0),因为过点
(a>b>0),因为过点 ,
,
所以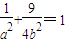 ①
①
又c=1,所以a2=b2+c2=b2+1 ②
由①②可得a2=4,b2=3.
故椭圆C的方程为 ;
;
(Ⅱ)证明:由(Ⅰ)知, ,所以
,所以 .
.
故设直线l: ,
,
联立 ,得x2+mx+m2-3=0.
,得x2+mx+m2-3=0.
∴ .
.
∴
=
= =1-1=0.
=1-1=0.
故直线MA,MB与x轴始终围成一个等腰三角形.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法和学生的计算能力,属难题.
(Ⅱ)由椭圆方程求出顶点N的坐标,求出MN的斜率,设出直线l的斜截式方程,和椭圆联立后利用根与系数的关系求出A,B两点的横坐标的和与积,由两点式写出MA和MB的斜率,作和后化为含有直线l的截距的代数式,整理得到结果为0,所以结论得证.
解答:(Ⅰ)解:设椭圆的方程为
 (a>b>0),因为过点
(a>b>0),因为过点 ,
,所以
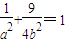 ①
①又c=1,所以a2=b2+c2=b2+1 ②
由①②可得a2=4,b2=3.
故椭圆C的方程为
 ;
;(Ⅱ)证明:由(Ⅰ)知,
 ,所以
,所以 .
.故设直线l:
 ,
,联立
 ,得x2+mx+m2-3=0.
,得x2+mx+m2-3=0.∴
 .
.∴

=

=
 =1-1=0.
=1-1=0.故直线MA,MB与x轴始终围成一个等腰三角形.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法和学生的计算能力,属难题.

练习册系列答案
相关题目
 (2013•临沂三模)已知椭圆C经过点M
(2013•临沂三模)已知椭圆C经过点M 已知椭圆C经过点M(1,
已知椭圆C经过点M(1, ),两个焦点是F1(-1,0)和F2(1,0)
),两个焦点是F1(-1,0)和F2(1,0)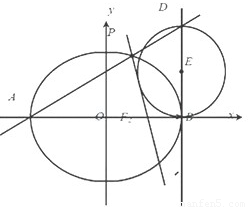
 ),两个焦点是F1(-1,0)和F2(1,0)
),两个焦点是F1(-1,0)和F2(1,0)