题目内容
已知二次函数 满足
满足 ,且
,且 .
.
(1)求解析式 ;
;
(2)当 时,函数
时,函数 的图像恒在函数
的图像恒在函数 的图像的上方,求实数
的图像的上方,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据二次函数 满足条件
满足条件 ,及
,及 ,可求
,可求 ,
, ,从而可求函数
,从而可求函数 的解析式;(2)在区间
的解析式;(2)在区间 上,
上, 的图象恒在
的图象恒在 的图象上方,等价于
的图象上方,等价于 在
在 上恒成立,等价于
上恒成立,等价于 在
在 上恒成立,求出左边函数的最小值,即可求得实数
上恒成立,求出左边函数的最小值,即可求得实数 的取值范围.
的取值范围.
试题解析:(1)由 ,令
,令 ,得
,得 ;令
;令 ,得
,得 .
.
设 ,故
,故 解得
解得 故
故 的解析式为
的解析式为 .
.
(2)因为 的图像恒在
的图像恒在 的图像上方,所以在
的图像上方,所以在 上,
上, 恒成立.即:
恒成立.即: 在区间
在区间 恒成立.所以令
恒成立.所以令 ,故
,故 在
在 上的最小值为
上的最小值为 ,∴
,∴ .
.
考点:1.函数的解析式求法;2.二次函数的图像与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
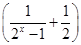 x3.
x3.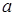 为正实数,函数
为正实数,函数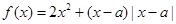 .
.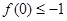 ,求
,求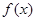 的最小值;
的最小值;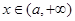 ,求不等式
,求不等式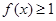 的解集.
的解集. ,函数
,函数 .
. 在
在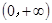 上单调递增;
上单调递增; .
.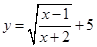 .
. 内有一动点
内有一动点 ,
, ,作
,作 于
于 ,
, 于
于 ,求矩形
,求矩形 面积的最小值和最大值,并指出取最大值时
面积的最小值和最大值,并指出取最大值时
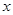 (百台),总成本为
(百台),总成本为 (万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入
(万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入 (万元),假定该产品产销平衡。
(万元),假定该产品产销平衡。 的图象经过点
的图象经过点 .
. 上的单调性,并用单调性的定义证明.
上的单调性,并用单调性的定义证明. 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有 (
( ,
, )成立,则称
)成立,则称 阶缩放函数.
阶缩放函数. 时,
时, ,求
,求 的值;
的值; ,求证:函数
,求证:函数 在
在 上无零点;
上无零点; 时,
时, ,求
,求 (
( )上的取值范围.
)上的取值范围.