Question

已知向量a=（1+cosα，sinα），b=（1-cosβ ，sinβ），c=（1，0），α∈（0，π），β∈（π，2π），a与c的夹角为θ₁，b与c的夹角为θ₂，且θ₁-θ₂=.求sin的值.

Answer 1

思路分析：解题目标——找出θ₁、θ₂与α、β的联系，不妨利用a·b=|a||b|cosθ试试?

解：∵α∈（0，π），β∈（π，2π），

∴|a|==2|cos|=2cos，

|b|==2|sin|=2sin，

|c|=1，a·c=1+cosα=2cos²，b·c=1-cosβ=2sin²，

∴cosθ₁=.

∵θ₁∈［0，π］，∈（0，）［0，π］，y=cosx的值在［0，π］上与x的值一一对应，∴θ₁=.

cosθ₂=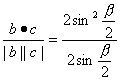

=sin=cos（-），

∵θ₂∈［0，π］，-∈（0，）（0，π），y=cosx的值在［0，π］上与x的值一一对应，

∴θ₂=-.又θ₁-θ₂=，

∴-+=，

∴=-，

∴sin=sin（-）=-.